☖ Home ⇄ Units Converter ⧉ Geometry Σ Math ✈ Physics 〶 Electricity

Free fall solved problems

Example 1 Example 2 Example 3 Example 4 Example 51 Example 52
Example 53 Example 55 Example 56 Example 54 Example 58
Example 57 Example 59 Two trajectories colision - Example 60 Trajectory along a slope - Example 61
Example 70 Object thrown from a car - Example 62 Free fall with wind effect - Two trajectories colision - Example 72 Vector calculation of trajectory - Two trajectories colision - Example 71
Rocket on a lunch pad - Example 67 Calculating the speed of sound - Example 63 Trajectories at same v0 and different angles - Example 64 Minimum v0 calculation - Example 65 Two angles for equal trajected distance - Example 66 Example 73
Horizontal trajectory - Equations summary Horizontal trajectort vector calculation
Calculating free fall problems notes Print notes about calculating free fall problems ▲
Free Fall
The velocity of a body falling to the earth in a vertical direction. (air resistance is not considered) are described by the equations:
(1a)
vt = v0 + g t(1b)
vt2 = v02 + 2 g h(1c)
Direction Variable signs
Upward motion −g    +t    +h    +v0    +vt
Downward motion −g    +t    −h    −v0    −vt
Always use the negative sign of    g = − 9.806 55   [m / s2]
Always use positive values of the time   t .
Values given v0 = vt = h = t =
v0     vt − −
h     t − −
v0     h − −
vt     h − −
t     v0 − v0 + g t −
t     vt vt − g t − −
Initial velocity [v0]: [m/s]
Final velocity [vt]: [m/s]
Height [h]: [m]
Falling time [t]: [s]
Vertical free fall - example 1 Print example 1 ▲
Example 1
A body is thrown upward with an initial velocity of  20 [m/s] . Find a) the highest point that it will reach and b) the time to reach this altitude and c) the time it reached half the height h.
a)
We know that the initial velocity  v0 = 20 [m/s]  and final velocity is
vt = 0 and we can find the maximum height according to the equation:
vt2 = v02 + 2 g h
b)
The time to reach the height is from eq.     vt = v0 + g t:
c)
In order to find the time to reach height h/2 we could solve the quadratic equation (1a) or to find the velocity at h/2 by eq. (1c) and then use eq. (1b)
Vertical free fall - example 2 Print example 2 ▲
Example 1
Figure 1
Example 1
Figure 2
Example 1
Figure 3
Ball  A  has dropped from a tower which is  200 m  above ground level from rest ,at the same time a second ball is thrown from the ground upward at an initial velocity of  80 [m ⁄ s].  Find the time and altitude of the bodies when they are passing each other, and find the minimum initial velocity upward of ball  B  in order to enable such a meeting.
We acknowledge that at the meeting point the altitude  h  and the travel time of both balls are the same.
For ball A: 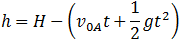(1)
For ball B: 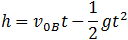(2)
Comparing both equations  (1)  and  (2)  we get the time to encounter  t:
Example 1
The meeting point altitude is from eq.  (2):
Example 1
Total falling time of ball A to the ground calculated by eq. (1a) is:
Example 1
The minimum upward velocity is when the two balls will meet at the ground level (see figure 3), it means that the maximum height of ball B will be reached after half the full falling time:     t = 6.4 / 2 = 3.2 [s]
v0B = vt − g t = 0 + 9.8 * 3.2 = 31.4 [m / s]
Another approach to calculate the time  t  until encounter (Figure 2) is to calculate the difference of the distance between ball A and ball B as a function of time by:
∆x = ( H − hA) − hB
Example 1
At the time of encounter of both balls    ∆x = 0     ->   t = 200 / 80 = 2.5 [s]
we get the same answer as before.
Vertical free fall - example 3 Print example 3 ▲
Example 3
Falling meeting point
Ball A is dropped from a  300 [m]  tower with an initial velocity of  20 [m/s],  at the same time a second ball is thrown from the ground upward at an initial velocity of  v0B [m/s].  Find the value of  v0B  if the two balls meet at a height of  100 [m]  above the ground.
From the question we know that ball  A  falls  200 m  with an initial velocity of  20 [m/s]  until it meets ball  B,  so the time to meeting can be calculated from equation.
Time until meeting
9.8 t2 + 40t − 400 = 0
t1, 2 = 4.67 , − 8.75
We take only the positive time  4.67 [s],  this time is also the falling time of ball  B  after throwing it upward so the initial velocity of ball B can be calculated from:
100=v_0B t-1/2 gt^2
v_0B=100/t+1/2 gt=100/4.67+(9.8∙4.67)/2=44.3 [m⁄s]
Horizontal free fall - example 4 Print example 3 ▲
Example 3
An object is thrown from the top of a building at a horizontal velocity of  vx [m/s],  the object heats the ground at a distance of  S = 100 [m]  from the building and with an angle of  θ = 35 ̊ . Find the height of the building and the horizontal velocity, suppose that the air resistance is negligible.
We have a combined motion in the  x  and  y  direction, horizontally the velocity is constant  vx = constant  and in the y direction we have free fall.
At impact point with the ground the vertical velocity is: vy = vx tanθ (1)
The equation for free fall with initial velocity is: vy2 = v02 + 2 g h (2)
From (2) we isolate  h,  the initial velocity downward is  0. h=v_y^2/2g=(v_x^2 tan^2⁡θ)/2g (3)
Falling time can be calculated from the equation: vy = v0 + g t
t=v_y/g=(v_x tan⁡θ)/g (4)
The distance traveled horizontally is equal to: S=tv_x=v_y/g v_x=(v_x^2 tan⁡θ)/g
v_x=√(gS/tan⁡θ )=√((9.8∙100)/tan⁡35 )=37.4 [m⁄s]
Substitute vx into eq.(1) we get the value of vy at ground.   v_y=v_x tan⁡θ=√(gS tan⁡θ)=26.2 [m⁄s]
Substitute  vy  or  vx  into  eq.(3)  to find  h: h=(S tan⁡θ)/2=35 [m]
Another way to solve the problem is by analyzing the trajectory path which is given by the equation:
y(x)=g/(2v_x^2 ) x^2
The trajectory angle at any distance from the building is: dy/dx=y^'=tan⁡θ=g/v_x^2 x
Insert the values  x = 100 [m]  and  θ = 35 ̊  we get: v_x=√(gx/tan⁡θ )=37.4 [m⁄s]
NOTE: we can find the value of  h  by energy method: mgh=1/2 mv_y^2
All potential energy at top of the building is converted to kinetic energy at ground level.
h=v_y^2/2g=(S tan⁡θ)/2
Horizontal trajectory - Example 51 Print example 51 ▲
Example 3
Note: g and vy in all calculations are negative.
In order to develop the trajectory path we get the motion equations
In the x direction constant speed:
x = v0 t (1)
In the y direction free fall motion:
y = g t2 / 2         (v0y = 0) (2)
From eq. (1) we get the value of the time: t = x / v0
Substitute the value of  t  into eq. (2) we get: y=g/(2v_x^2 ) x^2=kx^2 (3)
Any point on the trajectory path  y  is expresed by the displacement  x.  Because the value  g / (2 v02)  is a constant we can mark it for clarity as  k,  now we can see that the trajectory path is a parabola.
Trajectory velocity along the path is: V=√(V_x^2+V_y^2 )=√(V_0^2+g^2 t^2 )
Trajectory path angle θ is: θ=tan^(-1)⁡V_y/V_x =tan^(-1)⁡(gt/V_0 )
Total horizontal distance: D=V_0 √(2h/g)
Q
An object was dropped from an aircraft who is cruising horizontally at a height of  3 km  and a speed of  720 km/h. Find the distance from the dropping point and the angle of the object when it heats the ground, also calculate the angle that the pilot sees the target on the ground when he drops the object.
S
First convert the speed of  720 km/h  to  m/s            V0 = 720 * 1000 / 3600 = 200 m/s
Then from eq. (3) we get the impact distance: x=V_0 √(2y/g)=200√((2∙3000)/9.8)=4950 m
In order to find the impact angle we have to calculate the vertical velocity at ground level:
From eq. (1c): v_y=√2gh=√(2∙9.8∙3000)=242.5 m/s
And the impact angle is: θ=tan^(-1)⁡v_y/v_x = tan^(-1)242.5/200=50.5 deg⁡
The dropping angle is: α=tan^(-1)h/x tan^(-1)3000/4950=31.2 deg
Horizontal trajectory angle - Example 52 Print example 52 ▲
Example 3
Trajectory initial angle is θ0 and initial velocity V0
Horizontal distance at constant speed is:
x = V0 cosθ0 t (4)
Vertical height as a function of time from eq. (1a) is:
y = V0 sinθ0 t + g t2 / 2 (5)
Substitute  t  from  eq. (3)  to  eq. (4)  to get the trajectory path:
y=tan⁡θ x+g/(2V_0^2 cos⁡θ^2 ) x^2 (6)
This equation can be translated to     y = a x + b x2     so the trajectory path equation is a parabola.
We define the range  R  that is the distance traveled by the projectile until it returns to the same initial height, then from  eq. (6)  we have for  y = 0:
x (tan⁡θ+g/(2V_0^2 cos⁡θ^2 ) x)=0
The trivial solution x = 0 is at the origin and has no interest the second solution is the required range:
R=(-tan⁡θ 2V_0^2 cos⁡θ^2)/g=(-V_0^2 2 sin⁡θ cos⁡θ)/g=(-V_0^2 sin⁡2θ)/g (7)
The maximum range is when  θ = 45 °  then  sin2θ = 1  and the range is:       R = − V02 / g
Q
An object is thrown at a velocity of  20 m/s  at an angle of  30 deg.  Find the distance it heats the ground at the same height and the position of the object after  1.5 sec.
S
The vertical and horizontal velocity from eq. (1b) are:     (remember that g = − 9.8 m/s2)
vx = V0 cos30 = 17.3 m/s vy = V0 sin30 + g t
Total travel time can be calculated from (1b) t=2 (-V_0 sin⁡θ)/g=2 (-15 sin⁡30)/(-9.8)=1.53 sec
The range R that the object heats the ground is the time multyplied by  V0 cosθ:
R = t Vx = t V0 cosθ = 2.04 * 20 * cos30 = 35.34 m
The range can also be calculated by eq. (7): R=(-V_0^2 sin⁡2θ)/g=(-15^2 sin⁡60)/(-9.8)=19.88 m
The horizontal and vertical diatances after 1.5 sec are:
x(1.5s) = t V0 cosθ = 1.5 * 20 * cos30 = 25.98 m
y(1.5s) = t V0 sinθ + g t2 / 2 = 1.5 * 20 * sin30 − 9.8 * 1.52 / 2 = 3.97 m
The vertical velocity of the object from free fall eq. (1b)
vy(1.5s) = V0 cosθ + g t = 20 sin30 − 1.5 * 9.8 = − 4.7 m/s
Notice that  vy(1.5s)  is negative that is because the object passed the highest point and started to fall.
And the velocity of the object is: v=√(v_x^2+v_y^2 )=√(13^2+2.3^2 )=13.2 m/s
The direction of the velocity is: v=√(v_x^2+v_y^2 )=√(13^2+2.3^2 )=13.2 m/s
Horizontal trajectory angle - Example 53 Print example 53 ▲
Example 3
 A projectile is fired at a speed of 200 [m/s] at an angle of α = 20 [deg] from an inclined surface,the slope of the surface is θ = 30 [deg] from the horizontal.Find the distance d that the projectile will heat the inclined surface.
We mark the angle:       φ = θ + α = 30 + 20 = 50 °
The horizontal and vertical displacements are:
x = t V0 cosφ y = t V0 sinφ + g t2 / 2
after eliminating t from both equations we get: y(x)=x tan⁡φ+g/(2V_0^2 cos^2⁡φ ) x^2 (1)
From the inclined surface we have the relations: y(x) = d sinθ (2) x = d cosθ (3)
Substitute equations (2) and (3) into (1) gives: d sin⁡θ=d cos⁡θ tan⁡φ+g/(2v^2 cos^2⁡φ ) d^2 cos^2⁡θ
After rearanging the equation we get: d=([sin⁡θ-cos⁡θ tan⁡φ ]2v^2 cos^2⁡φ)/(g cos^2⁡θ )
d=([sin⁡30-cos⁡30 tan⁡50 ]∙2∙200^2 cos^2⁡50)/(-9.8∙cos^2⁡30 )=2393 m
Horizontal trajectory angle - Example 54 Print example 54 ▲
Example 3
 A ball is thrown at an angle  θ  relative to the horizon and with an initial velocity of  200 [m/s].  The ball should heat a target  450 [m]  above earth and at a distance of  2500 [m]  away. Find what should be the value of the angle  θ  in order to heat the target.
The trajactory path is defind by the equation:
y(x)=x tan⁡θ-g/2 x^2/(V_0^2 cos^2⁡θ ) (1)
In this equation all the parameters are known except the angle which can be found:
We will use the trigonometric identity: cos⁡θ=1/√(1+tan^2⁡θ ) into eq. (1)
y(x)=x tan⁡θ+(gx^2)/(2V_0^2 ) (1+tan^2⁡θ )
After arranging terms we get a quadratic equation with the unknown tanθ
(gx^2)/(2V_0^2 ) tan⁡θ+x tan⁡θ+(gx^2)/(2V_0^2 )-y(x)=0
After marking: z=(gx^2)/(2V_0^2 ) we get: u tan2θ + x tanθ + u - y(x) = 0
tan⁡θ=(-x±√(x^2-4z(z-y) ))/2z
θ=tan^(-1)⁡((-x±√(x^2-4z(z-y) ))/2z) (2)
Substitute the values given for the height distance and initial velocity we get:
u = − 765.6     and for the angle we get two values     θ = 30.7°    and    θ = 69.5°
V0 m/s
x m
h m
Range of θ that allows flying over the wall
Range of the distances d coresponding to the angles
Input limit:
Trajectory example
A vertical wall of  6 m  in height is located  30 m  from a projectile firing point, the projectile get an initial velocity of  20 m/s2  .Find the angle range that the projectile can be fired in order to pass the wall to the other side   (see calculator's Ex4).
According to eq. (2)         u = − 9.8 * 302 / (2 * 202) = − 11.025
θ=tan^(-1)⁡((-30±√(900-4(-11.025)(-11.025-6) ))/(-2∙11.025))
And the range of angles are: θ1 = 38.89° θ2 = 62.42°
The flight range according to the angles are:
d_1=(V_0^2 sin⁡(2θ_1 ))/g=(400 sin⁡(2∙38.89))/9.8=39.89 m
d_2=(V_0^2 sin⁡(2θ_2 ))/g=(400 sin⁡(2∙62.42))/9.8=33.5 m
Horizontal trajectory angle - Example 55 Print example 55 ▲
Example 3
An object is thrown upward on a slope and reached a height of  h = 15 m  as shown, the object heats the slope at a distance of  l = 75 m.  The slope angle α is 35°. Determine the magnitude  v  and the direction of the initial velocity.
The horizontal and vertical distances traveled are:
x = l * sinα = 75 cos35 = 61.4 m
y = −l * sinα = − 75 sin35 = − 43 m
The horizontal and vertical velocities of v are vx and v0y
From eq.  (1c)  the value of  v0y  is:
v_0y=√(-2gh)=√(2∙9.8∙15)=17.2 m/s
Total travel time from (1a): T=(-v_0y±√(v_0y^2+2gh))/g=(-17.2±√(17.2^2+2∙9.8∙43))/(-9.8)=-1.67 5.2 s
The horizontal velocity is: vx = x / T = 61.4 / 5.2 = 11.8   m/s
And the initial velocity is: v=√(v_x^2+v_0y^2 )=√(11.8^2+17.2^2 )=20.86 m/s
And the initial angle  θ  is: θ=tan^(-1)⁡v_0y/v_x=tan^(-1)17.2/11.8=55.5°
Horizontal trajectory angle - Example 56 Print example 56 ▲
Example 56
An anti aircraft gun start firing on an aircraft passing directly overhead with a muzzle velocity of 500 m/s the cruising velocity of the aircraft is 980 km/h and the altitude is 4 km. Find the firing angle and the time until it heats the aircraft.
The horizontal distance and the time traveled by the aircraft and the bullet until impact are the same:
For the aircraft     da = va t and for the bullet     db = v cosθ t
After dividing the diatance by time we get: da / t = db / t ⟶ va = v cosθ
After converting aircraft velocity to m/s we get: cosθ = va / v = 980 / (3.6 * 500) = 0.544
And the firing angle is: θ = cos − 10.544 = 57.02 °
The vertical initial velocity of the bullet is: v0b = v sinθ = 500 sin57.02 = 419.43 m/s
Total travel time can be calculated from eq. (1a):
t=(-v_0b±√(v_0b^2+2gh))/g=(-419.43±√(419.43^2-2∙9.8∙4000))/(-9.8)=10.93 , 74.66 s
We got two values but only the value   t = 10.93 s   is relevant because the second time is when the bullet returns to 6 km high after passing the highest point.
Horizontal trajectory angle - Example 57 Print example 57 ▲
Example 57
The horizontal velocity of an aircraft is 500 km/h at an altitude of 5.4 km. Find the angle that the pilot will see a car moving at a speed of 150 km/h horizontally in order to directly hit the car.
The projectile falling time until it hits the ground is from eq. (1a) where  v0y = 0:
t=√(2h/g)=√((2∙5400)/9.8)=33.2 s
Va km/h
Vc km/h
h m
θ
deg
t
s
D
m
d
m
Input limit:
The horizontal distance traveled by the projectile:
D = va t = 500 * 33.2/ 3.6 = 4611 m
At the same time the car traveled a distance of:
d = vc t = 150 * 33.2/ 3.6 = 1383.3 m
The angle θ will be:
θ=tan^(-1)⁡(h/(D-d))=tan^(-1)⁡(5400/(4611-1383.3))=59.13 °
Horizontal trajectory angle - Example 58 Print example 58 ▲
Example 58
A pilot releases a projectile while diving at an angle of θ = 40 degree and altitude of 2 km and a velocity of 600 km/h. Find the angle γ between diving line and the target as seen by the pilot at the release point.
The vertical and horizontal velocity of the aircraft ca be calculated from the speed and angle of the aircraft:
Horizontal: vx = v cosθ = 600 cos40 / 3.6 = 127.67 m/s
Vertical: v0y = v sinθ = 600 sin40 / 3.6 = 107.13 m/s
Falling time from eq. (1b) and (1c) is:
t=(v_ty-v_0y)/g=(√(v_0y^2+2gh)-v_0y)/g
t=(√(196.4^2+2∙9.8∙1800)-(-196.4))/(-9.8)=(±271.7+196.4)/(-9.8)=7.68
Horizontal trajectory travel distance: d = vx t = 600 cos40 * 12.04 / 3.6 = 1537.2 m
Angle α is equal to: α=tan^(-1)⁡h/d=tan^(-1)1800/1510.5=50 °
And the required angle ν is: γ = 180 − θ − (180 − α) = α − θ = 52.5 − 40 = 12.5 °
Horizontal trajectory angle - Example 59 Print example 59 ▲
Example 59
Find the maximum range that a projectile can reache for a muzzle velocity of 100 m/s and maximum height of 10 m.
v m/s
h m
R
m
θ
deg
t
s
vx
m/s
v0y
m/s
Input limit:
The initial vertical and horizontal velocities are:
v0y = v sinθ (1)
From eq. (1c) and with final vertical velocity  vty = 0  we get:
v_0y=√(-2gh) (2)
From (1) and (2) we get: sin⁡θ=√(-2gh)/v
and from trigonometric identity:
cos⁡θ=√(sin^2⁡θ-1)=1/v √(2gh-v^2 ) (3)
Flight time up and down from (1b) :
cos⁡θ=√(sin^2⁡θ-1)=1/v √(2gh-v^2 ) (4)
And the range is: R = vx t = v cosθ t = v 1/v √(2gh-v^2 ) ((-v) sin⁡θ)/g=1/g √(2ghv^2-4g^2 h^2 ) (5)
And the range numerically: R=(±√(2∙9.8∙10∙220^2-4∙9.8^2 10^2 ))/(-9.8)=627.3 m
Two trajectories Collision - Example 60 Print example 60 ▲
Example 60
Two objects  A  and  B  are located at a distance of  d  from each other, they are thrown at the same time, body  A  at an angle  θ  and initial velocity of  v0  and body  B  free falls from a height of H, both objects collide in midair at a height of  h  above ground. Find the angle  θ  and  v0  that will allow the collision.
We notice that the time from throw to collision for both objects are the same.
H m
h m2
d m
θ
deg
v0
m/s
t
s
α
deg
vc
m/s
Input limit:
The distance that object B falls is:         L = − (H − h) = h − H
Note: Because the direction of  L  is downward in order to keep compatibility with the free fall equations  L  should be negative and  H  and  h  are positive and  H > h.
The time to collision of B is from eq. (1a):
t_B=√(2(H-h)/g)
Distance traveled by object A: d = v0 cosθ tB (1)
Object A is reaching height h by the time  tB
h = v0 sinθ tB + g tB2 / 2 (2)
First we eliminate the values of v0 from both equations.
From eq. (1) v_0=d/(t cos⁡θ ) (3)
From eq. (2) we can elininate  v0 v_0=(2H-2h-gt^2)/(2t sin⁡θ ) (4)
From eq. (3) and (4) we have: v_0=d/(t cos⁡θ )
After substituting the value of tB into the equation we get: d/cos⁡θ =(2H-2h-g(2(H-h)/g))/(2 sin⁡θ )
Eliminating the angle value we have: sin⁡θ/cos⁡θ =tan⁡θ=(2h-2H+2h)/2d=H/d
And finally the angle is: θ=tan^(-1)⁡(H/d) (5)
And the value of  v0  from eq. (3) is: v_0=(gd^2)/(2(H-h) cos^2⁡θ ) (6)
Using the trigonometric equality to further develop we get: cos⁡θ=tan⁡θ/√(1+tan^2⁡θ )=H/√(d^2+H^2 )
Substitute the value of  cosθ  into eq. (6) we get the velocity of  v0 with H, h and d. v_0=d/H √(g (H^2+d^2)/2(H-h) )
Collision patern
The horizontal and vertical velocities at the collision are:
vcx = v0 cosθ and vcy = v0 sinθ + g tB
v_c=√(v_xc^2+v_yc^2 )=√(v_0^2 cos^2⁡θ+v_0^2 sin^2⁡θ+gv_0 t_B sin⁡θ+g^2t_B^2 )
tan⁡α=v_cy/v_cx =1/d (H+1/d √(2gd(H-h)^2 ))
Trajectory along a slope - Example 61 Print example 61 ▲
Example 60
A ball leaves a slope whose angle is  θ = 30 deg  with a velocity of  v0  the ball leaves the slope at a hight of h = 6 meter above the ground and hits the ground at a distance of  d = 10 meter.  Find the velocity  v0  expressed by  d, h and θ.
We will use the fact that the flight time vertically and horizontally is the same.
d m
h m2
θ deg
v0 m/s
t
s
v0x
deg
v0y
m/s
vt
m/s
α
deg
v0x = v0 cosθ and v0y = −v0 sinθ
In the horizontal direction the velocity is constant therefore:
d = t v0 cosθ and t=d/(v_0 cos⁡θ ) (1)
From the vertical free fall we have according to (1a):
h=v_0 sin⁡θ t+1/2 gt^2 (2)
Substitute the time from (1) into eq. (2) we get:
h=v_0 sin⁡θ d/(v_0 cos⁡θ )+1/2 g d^2/(v_0^2 cos^2⁡θ )
v_0=d/cos⁡θ √(g/(2h-2d tan⁡θ ))(3)
v_0=10/cos⁡30 √((-9.8)/2(5-10 tan⁡30 ) )=29.07 m/s
Notes: Remember that  h  and  v0y  are pointed down so they are negative values in the calculations. From geometric consideration   d < |h| / tanθ     (in the calculator input  h  can be negative or positive).
Q
If given the values of  d, h  and  v0  find the value of the slope angle  θ  of the example above.
S
From equation (2) all parameters are known except the angle θ. Multiplying all terms by  v02 cos2θ  we have:
From eq. (3) we have: cos^2⁡θ (2h+2d tan⁡θ )=(gd^2)/v_0^2 (4)
From trigonometric identity: cos^2⁡θ=1/(1+tan^2⁡θ )
Substitute cos2θ into (4) we have: 1/(1+tan^2⁡θ ) (2h+2d tan⁡θ )=(gd^2)/v_0^2
After arranging terms we get: (gd^2)/v_0^2 tan^2⁡θ-2d tan⁡θ+(gd^2)/v_0^2 -2h=0 (5)
We got a quadratic equation with the unknown  tanθ .           A tan2θ + B tanθ + C = 0
tan⁡θ=(-B±√(B^2-4AC))/2A where A=(gd^2)/v_0^2 B=-2d C=(gd^2)/v_0^2 -2h
Object thrown from a car - Example 62 Print example 62 ▲
Example 62
A small object is thrown at an angle of θ and initial velocity of v0 throught the complete flight a constant acceleration of a m/s2 is acting on the object in the negative flight direction. Finf the flight time and the distance of hit point on the ground.
The horizontal and vertical componants of the velocity are:
v0x = v0 cosθ and v0y = v0 sinθ
At the hightest point vty = 0 so the total flight time from (1b) is:
t=(-v_0y)/g=(-2v_0 sin⁡θ)/g (1)
Horizontally the velocity of the object is a mix of a constant velocity and a negative acceleration:
vtx = v0 cosθ + a t (2)
From equation (2) we can clearly see that when vtx = 0 the object changes the flight direction and t is.
t=(v_0 cos⁡θ)/a (3)
The final displacement d is according to eq. (1a) and the time from eq. (1):
t=(v_0 cos⁡θ)/a(4)
The maximum displacement dmax is according to eq. (1a) and the time of eq. (3):
Flight path
A: Flight when    tanθ > g / a
Flight path
B: Flight when    tanθ < g / a
 d_max=v_0 cos⁡θ (v_0 cos⁡θ)/a+1/2 a (v_0^2 cos^2⁡θ)/a^2
d_max=(3v_0^2)/2a cos^2⁡θ (5)
In equation  (4)  if we set  d = 0  then the object will return exactly to the throw point so we have the condition:
tan⁡θ=g/a
Q
Given v0 = 12 m/s θ = 60 ° and a = 8 m/s2. Find total flight time, the distance of the impact with the ground, what is the maximum distance in the x axis positive direction.
S
From eq. (1) we can find the total flight time: t=(-2∙15∙sin⁡53)/(-9.8)=2.44 s
Final displacement From eq. (4): d=(2∙15^2∙sin⁡53)/(-9.8) (-cos⁡53+sin⁡53 )=-7.2 m
From eq. (5) we can find the maximum displacement to the positive x axis:
v0 m/s
θ deg
a m/s2
d
m
dmax
m
α
deg
vt
m/s
t
s
h
m
d_max=(-15^2)/(-2∙10) cos^2⁡53=4.07 m
Final vertical velocity:
vty = − v0y = − 12 * sin60 = − 10.4 m/s
Final horizontal velocity:
vtx = v0x + at = 12 * cos60 − 8 * 2.12 = − 10.96 m/s
Velocity at ground impact:
v_t=√(v_tx^2+v_ty^2 )=√(11.98^2+14.88^2 )=19.1 m/s
Object ground hit angle:
α=tan^(-1)v_ty/v_tx=tan^(-1)⁡11.98/14.88=38.8°
Calculating the speed of sound - Example 63 Print example 63 ▲
Example 63
In order to calculate the speed of sound an object has been dropped from a height  h  of  50 m,  at the exact time of impact with the ground a timer on the top of the building at a height of  65 m  has been activated and measured the time that the sound was heard to be  T = 3.382 s.  Find the speed of sound.
From eq. (1a) and taking v0 = 0 the time of fall can be calculated
t=√(2h/g)=√((-2∙30)/(-9.8))=2.474 s
From the time of impact the sound reached the top after time  T:
H = vs Δt = vs (T − t)
v_s=H/(T-t)=38/(2.586-2.474)=340.3 m/s
Note:  this value of sound speed according to the table is measured at an outside temperature of  24 °C
Trajectories at same v0 and different angles - Example 64 Print example 64 ▲
Example 64
Two identical objects are trajected with equal initial velocities at the same time from point  A  but at a different angles. Verify  a) if the objects will collide at point  B  and  b) if the total flight time are the same and  c) if the absolute velocities of the objects at point  B  are the equal.
Object 1: v1x = v0 cosθ v1y0 = v0 sinθ
Object 2: v2x = v0 cosγ v2y0 = v0 sinγ
a) Let assume that the horizontal distance of point  B  is       d  for both objects, because  θ > γ  also  cosγ > cosθ
and from the horizontal velocities of the objects we see that v2x > v1x and because  d  is the same for both objects, object 2 will pass point B before object 1 and the objects will not collide at point B.
b) The total flight time of both objects are: T_1C=(-2v_0 sin⁡θ)/g T_2D=(-2v_0 sin⁡γ)/g
And we get the relationship between the times: T_1C/T_2D =sin⁡θ/sin⁡γ
c) the vertical velocities of the objects at point B according to eq. (1c) are:
v_t1^2=v_0^2 sin^2⁡θ+2gh v_t2^2=v_0^2 sin^2⁡γ+2gh
And the absolute velocities are:
v_t2^2=v_0^2 sin^2⁡γ+2gh
v_t2^2=v_0^2 sin^2⁡γ+2gh
We clearly see that the absolute velocities of objects 1 and 2 at point B are the same and are not a function of the angles.
Minimum v0 calculation - Example 65 Print example 65 ▲
Example 65
An object is thrown from a height  h  and at an angle of θ . Find the angle θ for a minimum initial velocity in order to fall at a distance  d,  what is the initial velocity in this case.
in the horizontal direction we have: d = v0 cosθ t (1)
From eq. (1a) in the vertical direction we have:
h=v_0 sin⁡θ t+1/2 gt^2 (2)
Substitute the value of  t  from eq. (1) into eq. (2) to get:
h=d tan⁡θ+(gd^2)/(2v_0^2 cos^2⁡θ ) (3)
In order to find the minimum angle we have first to express the velocity  v0 as a function of the angle  θ
From eq (3) we can find v0 v_0^2=(gd^2)/((h-d tan⁡θ )2 cos^2⁡θ )
After changing tanθ = sinθ / cosθ we get: v_0^2=(gd^2)/((h cos⁡θ-d sin⁡θ )2 cos⁡θ ) (4)
In order to find the angle that will give minimum initial velocity we will differentiate the right side of eq. (4) and compare it to zero. the power of  v0  don't make any difference because the minimum of  v0  is also the minimum of  v02 .
   (dv_0^2)/dθ=(2 sin⁡θ (h cos⁡θ-d sin⁡θ )-2 cos⁡θ (-h sin⁡θ-d cos⁡θ ))/[(h cos⁡θ-d sin⁡θ )2 cos⁡θ ]^2 =0
   2h sin⁡θ cos⁡θ-d sin^2⁡θ+d cos^2⁡θ=0
Dividing the last equation by cos2θ to get: d tan2θ − 2h tanθ + 2d = 0
And the solution of the quadratic eq. with  tanθ  is: tan⁡θ=(h±√(h^2+d^2 ))/d (5)
After the angle had been found we can use eq. (4) in order to find the minimum initial velocity v0 is.
For example if  h = 8 m  and  d = 8 m  then the angle of the minimum initial velovity is from eq. (5)
θ=tan^(-1)(-8±√(8^2+8^2 ))/8=-1±√2=22.5° -67.5°
And the correct solution is the positive angle  22.5°  and the initial velocity according to eq. (4) is:
v_0=d√(g/(2h cos^2⁡θ-d sin⁡2θ ))=8√(9.8/(2∙8∙cos^2⁡22.5-8 sin⁡45 ))=8.85 m/s
Two angles for equal trajected distance - Example 66 Print example 66 ▲
Example 66
For equal trajected distances of  d = 10 m  and initial velocities of  v0 = 12 m/s  there are two possible angles, find the ratio between the two flight times.
The horizontal and vertical initial velocities are:
vx = v0 cosθ v0y = v0 sinθ
In the horizontal direction: d = vx t = v0 cosθ t
And half flight time is t=d/(v_0 cos⁡θ ) (1)
v0 m/s
d m2
θ 1
deg
θ 2
deg
t1
s
t2
s
h1
m
h2
m
From eq.  (1c) h=(-v_0^2 sin^2⁡θ)/2g (2)
Substitute  t  and  h  into eq  (1a)  we get:
(-v_0^2 sin^2⁡θ)/2g=v_0 sin⁡θ d/(v_0 cos⁡θ )+1/2 g d^2/(v_0^2 cos^2⁡θ )
Multiplying all terms by   4gv02cos2θ  we get a quadratic equation with the unknown  sin2θ:
v04 sin22θ + 2 g v02 d sin2θ + g2 d2 = 0
The solution is simply: θ=1/2 sin^(-1)⁡((-gd)/v_0^2 ) (3)
And the angle is: θ=1/2 sin^(-1)⁡((-gd)/v_0^2 )
From trigonometry there is another solution to equation (3) that is:
sinθ2 = sin(π − 2θ1) ⟶ θ2 = π − 2θ1
From eq. (1) t_1/t_2 =cos⁡θ_2 /cos⁡θ_1 =sin⁡θ_1 /cos⁡θ_1 =tan⁡θ_1 or t_1/t_2 =cot⁡θ_2
Note: we use the relation: sin⁡(π/2-α)=cos⁡α g = − 9.8 m/s2
From the question we have: θ_1=1/2 sin^(-1)⁡((9.8∙10)/12^2 )=21.44°
And the ratio t1 / t2 is: t1 / t2 = tanθ1 = tan 21.44 = 0.39
Rocket on a lunch pad - Example 67 Print example 67 ▲
Example 67
A rocket is fired from a  30 degree  inclined launch pad and with an acceleration of  4 m/s2  when it pass point  A  which is at the ground level as point  C  his velocity is  vA  at point  B  which is  12 m  above ground level, the rocket's engine stop working and it continues flight at gravitational forces until it hits the ground at a distance of  d = 35 m.  Find the velocity of the rocket at point  A.
vA m/s
vB m/s
d m
h m
θ deg
a m/s2
H
m
tab
s
tbc
s
Vertical and horizontal velocity at point B are:
vBy0 = vB sinθ vBx0 = vB cosθ
The horizontal distance from  B  to  C  is equal to:
d = vBx0 tBC = vB cosθ tBC (1)
From the vertical direction from eq. (1a) we have:
h = vB sinθ tBC + g tBC2 / 2 (2)
And velocity  vB  is:
-h=v_B sin⁡θ d/(v_B cos⁡θ )+1/2 g d^2/(v_B^2 cos^2⁡θ )
After arranging terms we get:
vB2 (2 h cos2θ − d sin2θ) − g d2 = 0
And velocity  vB  is: -h=v_B sin⁡θ d/(v_B cos⁡θ )+1/2 g d^2/(v_B^2 cos^2⁡θ ) (3)
And velocity  vA  is: -h=v_B sin⁡θ d/(v_B cos⁡θ )+1/2 g d^2/(v_B^2 cos^2⁡θ ) (4)
Total flight time is: -h=v_B sin⁡θ d/(v_B cos⁡θ )+1/2 g d^2/(v_B^2 cos^2⁡θ ) (5)
Maximum altitude will be: -h=v_B sin⁡θ d/(v_B cos⁡θ )+1/2 g d^2/(v_B^2 cos^2⁡θ ) (6)
Substitute the numerical values of the question we get:
The velocity  vB  from eq. (3) is: v_B=√((-9.8∙35^2)/(-2∙12 cos^2⁡30-35∙sin⁡60 ))=15.76 m/s
And the velocity  vA at point A from eq. (4) is: v_A=√(15.76^2-2∙4∙12/sin⁡30 )=7.5 m/s
Total flight time from point  A  from eq. (5) is: T=(15.76-7.5)/4+35/(15.76∙cos⁡30 )=4.63 s
Maximum height from ground from eq. (6) is: H=(-15.76^2∙0.5^2)/(-2∙9.8)+12=15.17 m
Horizontal acceleration trajectory - Example 70 Print example 70 ▲
Example 70
A rocket lanched from an aircraft get an acceleration of 4 m/s2 the altitude and the velocity of the aircraft are 3000 m and 900 km/h respecteadly. Find the angle θ between the horizon and the line of sight to the target.
v0x m/s
ax m/s2
h m
θ
deg
d
m
t
s
α
deg
V
m/s
The total flight time from the free fall eq. (1a) is:
t=√(2h/g)=√((2∙3000)/9.8)=24.75 s
The horizontal movement is with constant acceleration and initial velocity of the aircraft.
The distance traveled by the rocket is:
d=v_0x t+1/2 at^2=(900∙24.75)/3.6+1/2∙4∙24.75^2=7412.6 m
And the angle θ is:
θ=tan^(-1)⁡h/d=tan^(-1)3000/7412.6=22.03°
Velocity and angle at hit point
At the hit point we have: vtx = v0x2 + 2 a d v_ty=√2gh
α=tan^(-1)⁡(v_ty/v_tx ) V=√(v_tx^2+v_ty^2 )
Horizontal acceleration trajectory - Example 72 Print example 72 ▲
Example 72
A small object is thrown from point  A  upward with an initial velocity of  25 m/s  near a building whose height is  15 m,  when the object passes point  B  it is subjected to a steady wind that accelerates the object by  3 m/s2  to the right. Find the distance from point B  to the hit point at  C  and the angle of the hit  γ.
The time and velocity at points  AB  can be calculated by free fall equations (g = − 9.8 m/s2).
The velocity upward of the object at point  B  according to free fal equation (1c) is:
v_B=√(〖v_0〗^2+2gh)=√(〖30〗^2-2∙9.8∙25)=20.25 m/s
vB is the initial velocity at point B, the time tB to reach the maximum height from point B is from (1b)
tB = (vt − vB) / g = (0 − 18.2) / (− 9.8) = 1.86 s
And the total flight time BC is: TBC = 2 tB = 2 * 1.86 = 3.72 s
In the horizontal direction we have an acceleration of  3 m/s2  and the initial velocity horizontaly at point  B  is  0,  the total distance traveled according to (1a) and changing  g  by the acceleration  a  is:
d = v0 TBC + a TBC2 / 2 = 0 * 3.72 + 3 * 3.722 / 2 = 20.5 m
The horizontal velocity at point C is: vcx = 0 + a TBC = 3 * 3.72 = 11.1 m/s
The vertical velocity at point C is: vcy = − vB = − 18.2 m/s
Angle γ is: γ = tan− 1 ( vcy / vcx) = tan− 1 (− 18.2 / 11.1) = − 58.6 deg
Horizontal trajectory - Equations summary Print example 3 ▲
Horizontal trajectory path
Notes:
vx is constant throuhout the trajectory.
Only in the following equations  g  is positive and equal to:     g = 9.80665 m/s2
(g  is positive in order to simplify the equations)
the trajectory equation is:
y(x)=x tan⁡θ-g/2 x^2/(V_0^2 cos^2⁡θ )
Horizontal constant velocity: Vx = V0 cosθ0 (1)
Vertical initial velocity: Vy0 = V0 sinθ0 (2)
tanθ_0=V_y0/V_x and V_0=√(V_y0^2+V_x^2 )
From vertical free fall: Vy = Vy0 = V0 sinθ − g t (3)
Velocity magnitude along flight path: V=√(V_0^2-2gtV_0 sinθ_0+g^2 t^2 ) (4)
Distance horizontal:  d=d(t): d = Vx t = V0 cosθ0 t (5)
Range total: R=(V_0^2 sin2θ_0)/g=(2V_x V_y0)/g (6)
Range maximum  (θ=45°) R_max=V_0^2/g (7)
Altitude vertical:  y=y(t) y=V_0 sinθ_0 t-1/2 gt^2 (8)
Altitude maximum: H=-V_y0^2/2g=-(V_0^2 sin^2θ_0)/2g (9)
Travel time upward: t_u=-(V_0 sin⁡θ_0)/g=-V_y0/g (10)
Travel total time (up+down): t=2 t_u=-(2V_0 sin⁡θ_0)/g=-(2V_y0)/g (11)
Angle initial: θ_0=1/2sin^(-1)⁡(-(R g)/V_0^2 )=tan^(-1)⁡(V_y0/V_x ) (12)
Angle  θ  throuhout the flight: θ=tan^(-1)⁡(V_y/V_x )=tan^(-1)⁡((V_0 sin⁡θ_0+gt)/(V_0 cosθ_0 )) (13)
x as a function of  y: x=V_x/g (V_y0±√(V_y0^2-2gy)) (14)
Time of flight as a function of  y: t=V_y0/g±√(V_y0^2/g^2 +2y/g)=1/g (V_y0±√(V_y0^2+2gy)) (15)
Horizontal trajectort vector calculation Print example 70 ▲
Location vector
Any point along the path of a projectile can be described by a location vector  r(t) that is a function of time  t.  The notation i and j denotes the unit vector in the x and y direction
r ̅=(r_x ) ̅i+(r_y ) ̅j
The velocity vector is the derivation of the location vector according to time t therfore we have:
v ̅(t)=(d(r_x ) ̅(t))/dt i+(d(r_y ) ̅(t))/dt j
The acceleration is the derivation of velocity: a ̅(t)=(dv ̅(t))/dt=(d(r_x ) ̅^2 (t))/(dt^2 ) i+(d(r_y ) ̅^2 (t))/(dt^2 ) j
In horizontal trajectory we have constant speed in the x direction and free fall in the y direction so the location vector will be:
r ̅=v_0 cos⁡θ ti+(v_0 sin⁡θ t+1/2 gt^2 )j
The velocity is: v ̅(t)=(dr ̅(t))/dt=v_0 cos⁡θ i+(v_0 sin⁡θ+gt)j
The acceleration is: a ̅(t)=(dv ̅(t))/dt=gj
The direction of the velocity is tangent to the trajectory curve and is equal to the tangent:
tan⁡θ=v_y/v_x =(v_0 sin⁡θ+gt)/(v_0 cos⁡θ )
The magnitude of the velocity is: v=√(v_x^2+v_y^2 )=√(v_0^2+2v_0 sin⁡θ gt+g^2 t^2)
Note the benefit of the vector trajectory calculation is that three dimensional systems can be easily calculated we have only to add the z direction or k unit vector and make the same calculations.
Vector calculation of trajectory - Example 71 Print example 71 ▲
Q
The  x  and  y  coordinate of a moving partical is given by  x = 2t2 + 3t  and  y = 2t3 + 2t − 5  where  x  and  y  are in meters and  t  in seconds. Find the magnitude and the direction of the velocity and the acceleration at the point when  t = 2  seconds.
S
The velocity along the path is: v ̅=dx/dt i+dy/dt j=(4t+3)i+(6t^2+2)j
The velocity after 2 seconds is: v ̅_(t=2)=11i+26j
The magnitude of the velocity is: v=√(v_x^2+v_y^2 )=√(11^2+26^2 )=28.23 m/s
The direction of the velocity is: θ_v=tan^(-1)⁡(v_y/v_x )=tan^(-1)⁡(26/11)=67.07 °
The acceleration along the path is: a ̅=(dv ̅)/dt=(d^2 x)/(dt^2 ) i+(d^2 y)/(dt^2 ) j=4i+12tj
The acceleration after 2 seconds is: a ̅_(t=2)=4i+24j
The magnitude of the acceleration is: a=√(a_x^2+a_y^2 )=√(4^2+24^2 )=24.33 m/s^2
The direction of the acceleration is: θ_a=tan^(-1)⁡(a_y/a_x )=tan^(-1)⁡(24/4)=80.54 °
Three dimantional free fal - Example 73 Print example 73 ▲
Example 73
A small object is located at point  r0 = 2i + 3j  at time  t = 0  it is trajected with an initial velocity of  v0 = 8i + 6k  if air resistance is neglected find the velocity and the location of the object after 3  seconds.
From eq. (1b) the velocity is vt = v0 + g t so we get in vector form.
vt = 8i + 6k + gtk = 8i + (6 + gt)k
The velocity and the magnitude after 3 seconds are:
vt=3 = 8i + (6 − 9.8 * 3)k = 8i − 23.4 k
|v|_(t=3)=√(8^2+23.4^2 )=27.73 m/s
The location of the object as a function of time from eq. (1a) is:
rt = r0 + v0t + gt2 / 2
rt = 2i + 3j + 8i + 6k + (gt2 / 2)k = 10i + 3j + (6 + gt2 / 2)k
rt=3 = 10i + 3j + (6 − 9.8 * 32 / 2)k = 10i + 3j − 38.1k   m
|r|_(t=3)= √(10^2+3^2+82.2^2)=82.86 m