☖ Home ⇄ Units Converter ⧉ Geometry Σ Math ✈ Physics 〶 Electricity

Friction and pulleys solved problems

Example 1 Example 2 Example 4 Example 5 Example 5a Example 6 Example 7
Example 9 Example 11 Example 12 Example 13 Example 14 Example 15 Example 16
Example 17 Example 21 Example 24 Example 33 Example 37 Example 38 Example 40

Calculating friction and pulley problems notes

Print calculating friction notes
According to the second law of motion we have F = m a
In the gravitational system the force acting on a mass is W = m g [kgm m / s2 ]
A force of 1 Newton is equal to N = 1 [kgm m / s2 ]
Then if the weight is given it equals W [kgf ] = 9.8 N
There are two friction coefficients the static μs and the dynamic or kinetic μk
The static friction coefficient value is greater then the kinetic coefficient value ( μs > μk ), it means that we have to employ greater force in order to start the movement of the mass, but once the mass is moving we have to employ less force to keep it moving. In many problems we assume that both coefficients are the same, if not we have to relate to the proper coefficient e.g. if the bodies are moving, we must take the kinetic friction coefficient.
Direction of acceleration and the friction force
The normal force on a mass is equal to   N = mg
The maximum friction force at rest is:   fs = Nμs = mgμs

Once the mass starts to move the friction force reduces to   fk = Nμk

To find the acceleration  a  of mass  m  we have to calculate the kinetic friction forces. From forces at the  x  direction we have:

Nμk = ma     →     mgμk = ma     →     a = gμk

Various materials static and kinetic friction coefficients

Material
On surface
Condition
μs
μk
Steel
Steel
Dry
0.76
0.42
Steel
Copper
Dry
0.53
0.36
Steel
Aluminum
Dry
0.61
0.47
Steel
Teflon
Dry
0.04
0.04
Cast iron
Cast iron
Dry
1.1
0.15
Cast iron
Cast iron
Lubricated
0.2
0.07
Aluminum
Aluminum
Dry
1.4
0.82
Teflon
Teflon
Dry
0.04
0.04
Nylon
Nylon
Dry
0.2
0.15
Ice
Ice
0º C
0.1
0.04
Rubber
Concrete
Dry
1
0.8
Rubber
Concrete
Wet
0.3
0.25
Glass
Glass
Dry
0.94
0.4
Wood
Wood
Dry
0.35
0.2
Waxed Wood
Snow
Dry
0.1
0.04
Note: the values presented in the table are mean values, as the friction coefficients are depending on many factors as specific type of material, type and quantity of lubricant, surface roughness and many more.
Direction of acceleration and the friction force
In many cases we must decide the direction of the movement, it is important because the direction of the friction force is always opposite to the movement direction.
If we look at the figure at left the direction of the movement is to the right as the direction of a1 the equilibrium equation will be:
ΣFx = F − m g sin θ − f = m a
and the acceleration is: Acceleration value movement to the right
Opposite direction of acceleration and friction force
If the movement is downward as in the second figure at left, then the equilibrium equation will be:
ΣFx = m g sin θ − F − f = m a
and the acceleration is: Acceleration value movement to the left
We can clearly see the difference of the signs and the values of the accelerations in both direction of the chose directions.
The conclusion from this calculation is that in friction problems a negative acceleration result doesn't mean that the acceleration is in the opposite direction but rather we have to change the direction of the acceleration and solve again, if this time we got negative value then the mass will not move due to the friction force, for more information see example 7, example 38.
Acceleration of two masses connected by pulley
If mass M is moving a distance of x meter, then this distance is divided by each cable that holds mass m and mass m is moving a distance of x/2 meter.
The distance travelled is given by:         x = v0 t + a t2 / 2
At rest v0 = 0 and the acceleration is:       a = 2 x / t2
time t of both masses M and m is the same so we can see that the acceleration is related to the distance, if the distance is half also the acceleration will be half so:     a1 = 2 a2
For system rest we need that the acceleration will be   0.  From the equation   vt = v0 + a t   we get the result   vt = v0
Friction example - 1 Print example 1 ▲
Friction on slope - example 1
Free body diagram of example 1
 A body whose mass is  m  is resting on an inclined surface with an angle of  θ  and a friction coefficient of  μ, find the acceleration of the mass  m  as a function of  μ  and angle  θ.
From equilibrium in the  x  and  y  direction we get:
ΣFx = m g sinθ − N μ = m a (1)
ΣFy = N − m g cosθ = 0 (2)
From eq. (2) N = m g cosθ
Substitute N into eq. (1) m g sinθ − m g μ cosθ = m a
And the acceleration is: a = g( sin θ − μ cos θ)
When the system is at rest   a = 0   then: Friction coefficient of a tilted surface
We can see that the friction coefficient for rest condition must be equal or greater than the tangent of the slope   μ > tan θ.
Friction example - 2 Print example 2 ▲
Friction example 2
Free body diagram
Free body diagram with F = 0
 A body whose mass is  m  is resting on a horizontal surface whose friction coefficient is  μ, a force F is implied on the mass at an angle of  θ  degree. Find the acceleration of mass  m  and the maximum force that the mass  m  will still be at rest.
From the forces diagram we can derive the equilibrium equations:
ΣFx = F cos θ − Nμ = ma (1)
ΣFy = N + F sin θ − mg = 0 (2)
From eq. (2) N = mg − F sin θ
Substitute N into eq. (1) F cos θ − mgμ + Fμ sin θ = ma
Solving for  a  we get: 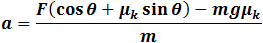Acceleration (3)
For the maximum force  F  that can be applied so that the mass  m  will still be at rest we have:
fmax = N μs = (m g − F sinθ) μs(4)
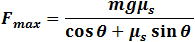Maximum F for rest condition(5)
A force of 30 N is applied to a mass of 3 kg for 5 sec at an angle of 30 degree, if the static and kinetic frictions are 0.5 and 0.2 respectively. Find the acceleration and the time needed for mass  m  to stop after force F is eliminated.
First check if the mass will move by the condition:   fmax < F cosθ.
Because  7.2 < 25.98  the mass will move and the acceleration is according to equation (3).
Acceleration of case F = 0
The velocity of the mass after 5 sec is found from the acceleration aquation:
vt = v0 + a t = 0 + 7.7 * 5 = 38.5 m/s
The new free body diagram after eliminating force F is at left.
According to the second law of motion   F = m a (F  now is only the friction force) and   f = − m a  (the minus sign is because of the opposite directions of  a  and  f).
a = − f / m = − m g μk / m = −g μk = − 9.8 * 0.2 = − 1.96 m/s2
And the time until mass m will stop is according to the equation:   vt = v0 + a t   where    vt = 0    and    v0 = 38.5 m/s
t = − v0 / a = − 38.5 / − 1.96 = 19.64 sec
Friction of two masses - example 4 Print example 4 ▲
Example 4
Free body diagram
 Two masses are located on each other, mass  m  is tied to the wall by a rope, a force  F  is exerted on mass  M , find the acceleration of mass  M  if the friction coefficients between the two masses is  μ1  and  μ2  between mass  M  and the lower surface.
Friction force f1 is: f1 = mgμ1
Friction force f2 is: f2 = (M + m)gμ2
Mass M is affected by both frictions f1 and f2 and is:
fM = f1 + f2 = mgμ1 + (M + m)gμ2
From the forces diagram we can derive the equilibrium equations in the x direction on both masses:
On mass  m: ΣFx = T1 − mgμ1 = 0 (1)
On mass  M: ΣFx = F − f1 − f2 = Ma (2)
Friction example 1
Maximum force F that can be applied to mass  M  without sliding is:
F <= mgμ1 + (M + m)gμ2
From eq (1)  T1  can be found: T1 = mgμ1
Friction of two masses example - 5 Print Fourier Series ▲
Friction example 5 Free body diagram of m1 Free body diagram of m2
Mass  m1  is resting on mass  m2  and has a friction coefficients of  μ1S   μ1k  the friction coefficients of  m2  and the lower surface are  μ2S  μ2k . Find the biggest force  F  that can be applied to  m2  without causing mass  m1  to slip.
m1 kg
m2 kg
μ1S
μ1k
μ2S
μ2k
F N
a1
m/s2
a2
m/s2
f1
N
f2
N
Force needed to start moving the masses is:     F = (m1 + m2) g μ2S
Mass  m1  is attached to  m2  only by the maximum friction force which is:  f1 = m1 g μ1S     this force is causing mass  m1  to accelerate to its maximum value before slipping:
ΣFx on m1 m1 g μ1S = m1 a1 ⟶ a1 = g μ1S (1)
From the free body diagram of mass m2 we have
ΣFx on m2 F − f1 − f2 = m2 a2
F − m1 g μ1S − (m1 + m2) g μ2k = m2 a2 (2)
Solving for the value of  a2  from eq. (2) we get:
Friction example 1     (3)
In order to prevent from mass  m1  to slip both accelerations  a1  and  a2  should be the same   a1 = a2   and the maximum force  F  is:
F = (m1 + m2)(a1 + g μ2k)     (4)
If the applied force  F  is greater then the value of  F  in eq. (4) then the mass m1 will slide on top of mass m2 and the friction force f1 will be the dynamic force which is less then the static force because μs > μk  so the forces on mass m2 in this case is:
F − m1gμ1k − (m1 + m2)gμ2k = m2 a2
Q.
Mass of 3 kg is mounted on top of a 7 kg mass, the friction coefficients of the upper mass are μ1S = 0.8 and μ1k = 0.1 and the lower mass friction coefficients are μ2S = 0.2 and μ2k = 0.1 . Find the maximum force F in case that mass m1 will not slide.
S.
First find the maximum acceleration acting on m1 with no slipping according to eq. (1):
a1 = g μ1S = 9.8 * 0.8 = 7.84 m/s2
This is also the maximum acceleration of mass m2 according to eq. (4) with the assumption that   a1 = a2
F = (m1 + m2)(a1 + g μ2k) = 88.2 N
Friction of two masses example - 5a Print Fourier Series ▲
Friction example 1
Friction example 1
Friction example 1
 Mass  m1  is located on mass  m2  Force F is applied on the upper mass, analyse the forces acting on the masses and the accelerations.
The maximum friction force acting on m1 is
f1s = N1μ1s = m1 g μ1s
The maximum friction force acting on m2 is
f2s = N2μ2s = (m1 + m2) g μ2s

If the force F is gradually increased and f2s > f1s, the friction force f1s is also increased to the maximum value of f1s = m1 g μ1s from this point on, increase of F will cause mass m1 to accelerate and the friction coefficient to decrease to the kinetic value μ1k. In this case the lower mass m2 will not move at all (Because mass m2 should move only by the friction force f1 but lower friction force is greater).

From the forces free body diagram in the x direction, mass m1 will move when force F overcomes the static friction force   f1 .
ΣFx   →     F − f1 = m1 a1
F − m1 g μ1S = m1 a1
(1)

Once force F is bigger then f1s then mass   m1   will accelerate by:

Friction example 1

If we want to enable mass m2 to move, then the maximum friction coefficient between mass m2 and the surface is calculated from the forces diagram in the x direction of mass m2, we have:

ΣFx   →     f1 − f2 = m2 a2
m1 g μ1s,k − (m1 + m2) g μ2s,k = m2 a2
(2)

Note   The values of μ is determined from the movement conditions, if the mass is not sliding then take the static values and if the mass is sliding then take the kinetic values of friction.

a) In order to keep both masses moving together we have to fulfil the condition that  a1 = a2 and remember that f1 is the static force between masses m1 and m2 and f2 is the kinetic force between mass m2 and the surface, then from equations 1) and 2) we get:

Friction example 5a
(3)
Friction example 5a
(4)
Q.
Mass  m1  of 3kg is located on mass  m2  of 7kg. The friction coefficients of m1 are  μ1s = 0.8   and  μ1k = 0.1   the friction coefficients of  m2  and the lower surface are  μ2s = 0.2  and  μ2k = 0.1   Find the biggest force  F  that can be applied to the upper mass  m1  without causing mass  m1  to slip.
S.
Maximum friction force between m1 and m2 is: f1s = m1 g μ1s = 3 * 9.8 * 0.8 = 23.52 N

minimum friction force between m2 and the surface is: f2k = (m1 + m2) g μ2k = (3 + 7) 9.8 * 0.1 = 9.8 N

From mass m2 we have:
Friction example 5a

And F is calculated from m1:     F = m1(a1 + g μ1s) = 3 (1.96 + 9.8 * 0.8) = 29.4 N

Remember that   a1 = a2   because both masses are travelling at the same speed.
Two masses and pulley - example 6 Print example 6 ▲
Example 6
Free body diagram
 Find the acceleration of the system of masses neglecting the mass of the string and the inertia of the pulley.
The kinetic friction force is equal to: f = μk N = μk M g
From the free body diagram on mass  m  and  M  and assuming that the acceleration is downward we get:
On mass M: ΣFx = T − M g μk = M a (1)
On mass m: ΣFy = m g − T = m a (2)
Eliminating  T  from both equations gives:
m g − M g μk + M a = −m a
Two masses and pulley(3)
Mass M will accelerate when m > μs M
System of the masses are at rest when m <= μs M     (then a = 0)
Find the friction coefficient and the tension in the rope if  M = 5 kg and  m = 1 kg  the masses are moving at a constant speed.
Because the masses are moving at a constant speed it is necessary that  a = 0. from eq.   (3)   we have     m − M μk = 0
Two masses and pulley
The tension in the rope can be found by solving eq.  (1)  and  (2) :
Two masses and pulley
Two masses and pulley - example 7 Print example 7 ▲
Example 7
Free body diagram acceleration to the right
Figure 1
Free body diagram acceleration to the left
Figure 2
M kg
m kg
θ deg
μ
a m/s2
T
N
f
N
Find the acceleration of the system of masses, the masses of the rope and the pulleys are negligible, assume first that the acceleration of  M  is upward and second time that the acceleration is downward.
The friction force is equal to: f = μ N = μ M g cosθ
From the forces diagram on mass  m  and  M  and assuming that the acceleration is upward (Figure 1) we get:
On mass M: ΣFx = T − M g sinθ − f = M a (1)
On mass m: ΣFy = m g − T = m a (2)
Friction example 1 (3)
Solving the case with the acceleration downward (Figure 2).
On mass M: ΣFx = M g sinθ − T − f = M a (4)
On mass m: ΣFy = T − m g = m a (5)
Friction example 1 (6)
Check the case when  M = 2 kg   m = 1.2 kg  angle  θ = 30  degree and the friction coefficient is  0.15
Friction example 1
Friction example 1
Because both accelerations in both directions are negative motion is not possible in these conditions of masses, friction and slope angle (see note 2).
Determine the acceleration and the motion direction if  M = 4 kg
m = 2 kg  angle  θ = 45  degree and the friction coefficient is  0.1
First check the case of upward acceleration (Figure 1).
Friction example 1
Because a is negative and the present of friction we have to make the calculation again assuming this time that the acceleration is downward see the case of (Figure 2).
Friction example 1
Notice that we got a different value for the acceleration, the conclusion is that mass  M  is sliding downward.
Note 1: from eq. (3) and (6) and comparing the acceleration to zero we can derive the range of mass m

that the system will stay at rest.               M(sinθ − μ cosθ) < m < M(sinθ + μ cosθ)
Note 2: to determine the direction of the motion we can solve the equilibrium equation by eliminating the friction, once we have the direction of the motion, we can set the correct direction of the friction force (always opposite to the motion direction) and solve the equilibrium equations. We have to remember that if we found motion in any direction without friction, the friction force can reduce the motion acceleration or even stope the motion.
Two masses on inclined surfaces   example - 9 Print example 9 ▲
Friction example 9 Free body diagram when acceleration is to the right
Find the acceleration of the system of masses neglecting the mass of the rope and the inertia of the pulley, the frictions coefficients and the slopes are given, also find the tension in the rope.
To determine the possible direction of the motion we will first solve the forces equations by neglecting the frictions, the results are the conditions:
m sinβ > M sinα motion can be to the right (a)
m sinβ < M sinα motion can be to the left (b)
m sinβ = M sinα motion not possible (c)
Those conditions alone are not enough to verify if the system will move, in order to make the system to slipe the masses have to overcome the friction forces, so the conditions for motions are.
m ( sinβ − μ2s cosβ ) > M ( sinα + μ1s cosα ) motion is to the right (d)
M ( sinα − μ1s cosα ) > m ( sinβ − μ2s cosβ ) motion is to the left (e)
From the forces diagram and assuming that the acceleration is to the right we get:
On mass M: ΣFx = T − M g sinα − M g cosα μ1k = M a (1)
On mass m: ΣFx = m g sinβ − T − m g cosβ μ2k = m a (2)
Acceleration when motion is to the right
System is at rest when: m(sinβ − μ2scosβ) − M(sinα + μ1s cosα) = 0
Tension when motion is to the right
In order to get positive tension in the rope we need that at least one of the equations will be true:
μ1s < tanα or μ2s < tanβ
Free body diagram when acceleration is to the left
Given two masses  M = 40 kg  and  m = 20 kg,  connected with an ideal pulley, the masses are located on two surfaces whose friction coefficients are μ1s = μ1k = 0.15 and μ2s = μ2k = 0.25, the slopes has angles of  α = 30 deg  and  β = 53 deg.  Find the direction and the value of the acceleration and the tension in the rope which connects both masses.
M kg
α deg
m kg
β deg
μ1s
μ1k
μ2s
μ2k
a
m/s2
T
N
No friction move:
Each mass move:
M m
System move:
First determine the possible motion direction according to criteria (a) and (b)
m sinβ = 20 sin53 = 16 < M sinα = 40 sin30 = 20
The direction of the acceleration will be to the left.
Now check criterion (c) and (d) to verify is motion occurs:
Motion equations for the case with acceleration to the left are:
On mass M: ΣFx = M g sinα − T − M g cosα μ1k = M a (3)
On mass m: ΣFx = T − m g sinβ − m g cosβ μ2k = m a (4)
Because we already found that the motion is to the left, we must check condition (d) only and we get 14.8 > 12.9 so the masses will slip to the left and the acceleration is:
Acceleration when motion is to the left
Tension when motion is to the left
Friction of two masses and pulley - example 11 Print example 11 ▲
Example 11 Free body diagram of the system
Free body diagram of mass m Free body diagram of mass M
Find the acceleration and the tension in the rope of the system of masses shown (M > m), neglecting the mass of the string and the inertia of the pulley assume that the static and kinetic friction coefficients are equal to  μ1   μ2  and the slope angle  θ  are known.
Notice that the two masses are moving in the opposite directions so the friction forces are:
Friction forces on mass M are: f1 = (M + m)gμ1 cosθ
Friction forces on mass m are: f2 = mgμ2 cosθ
From the forces diagram on mass  m  and  M  and assuming that the acceleration of mass  M  is downward and is equal to the acceleration of mass  m  in the upward direction we get:
On mass m ΣFx = T − f2 − mg sinθ = ma (1)
On mass M ΣFx = Mg sinθ − f1 − f2 − T = Ma (2)
Substitute the values of  f1 and f2  into eq. 1 and 2 and eliminating T from both equations we get  a:
Acceleration of the masses
Tension in the string
Two masses on pulley - example 12 Print example 12 ▲
Example 12 Free body diagram
Find the acceleration of the system of masses neglecting the mass of the rope and the inertia of the pulley.
From the forces diagram on mass  m  and  M  and assuming that the acceleration is to the downward direction of mass  M  we get:
On mass  M: ΣFy = Mg − T = Ma (1)
On mass  m: ΣFy = T − mg = ma (2)
Solving for the acceleration we get: Friction example 1
And the tensions in the cables are: Friction example 1 Friction example 1
Friction of two masses and pulley - example 13 Print example 13 ▲
Example 13 Free body diagram m1 and m2 Free body diagram of the pulley
Find the acceleration of the system of masses neglecting the mass of the rope and the inertia of the pulley, the friction coefficient between mass  M  and the surface is  μ.
From the forces diagram on mass  m  and  M  and assuming that the acceleration is to the downward direction and notice that the acceleration of mass M is twice the acceleration of mass m because when mass M is moving a length of x mass m will travel only half this distance.
Forces on mass  M: ΣFx = T − Mgμ = Ma1 (1)
Forces on mass  m: ΣFy = mg − T1 = ma2 (2)
From acceleration: a1 = 2a2 (3)
From the pulley: T1 = 2T (4)
We got four equations with four unknowns  T   T1  a1  and  a2 ,  solving the equations we get:
The accelerations are: Friction example 1 Friction example 1
The tensions are: Friction example 1 Friction example 1
Two masses and two pulleys - example 14 Print example 14 ▲
Example 14
Free body diagram
 Find the acceleration of the system of masses neglecting the mass of the rope and the inertia of the pulleys.
Forces on pulley 1: ΣFy = 2T − Mg = Ma1 (1)
Forces on mass  m: ΣFy = mg − T = ma2 (2)
Acceleration’s balance: a2 = 2a1 (3)
The relation between the accelerations can be found by measuring the distances that the masses travels, while mass  m  is moving a distance of  x  mass  M  will move a distance of  x/2  so the acceleration of  M  is half the acceleration of  m.
Solving for a1 a2 and T we get:
Friction example 1 Friction example 1
And the tension in the rope is: Friction example 1
The tension  T  is uniform along the cable.
The value of  T1  is: T1 = 2T
Notice that if we apply a force  F  downward at mass  m  we could lift a mass of  2F,  so this system multiplies the force by 2.
Friction of two masses example - 15 Print Fourier Series ▲
Friction example 15
Find the accelerations of masses m of 3kg and M of 4kg if a) there is no friction and b) find the accelerations if the static and kinetic friction coefficients are 0.3. Neglect the mass of the string and the inertia of the pulley and assume that the angle κ is steady along the movement.
Forces diagram
N = mg − T Sinθ
f = N μ = (mg − T Sinθ) μ
ΣFx on mass  m: T cosθ − (m g − T sinθ)μ = m a / cosθ (1)
ΣFy on mass  M: M g − T = M a (2)
The term  a cosθ  in equation (1)  is because the acceleration of the two masses are different, the acceleration of mass  m  is coincide with the direction of the tension  T  while the actual acceleration is along the  x  axis.

From equations 1 and 2 we can find the general solution with friction of the tension and the acceleration  a  of mass M .

Friction example 1

Acceleration of mass  m  is:        am = a / cosθ        (in the x direction)

acceleration values
Figure 3
If the rope is moving a distance of  x  downward with mass  M, then the same distance is moving mass m but the direction of movement is along the rope. this means that the distance travelled along the  x  axis is  x/cosθ  because the travelled time of masses  m  and  M  are the same the acceleration in the  x  direction of mass  m  is am = a/cosθ

The forces balance in the x direction without friction is:     T cosθ = m am = ma / cosθ

The forces balance in the x direction is:     Mg − T = Ma

And the acceleration a is:
a=g (M cos^2⁡θ)/(m+M cos^2⁡θ )=9.8 (2 cos^2⁡30)/(3+2 cos^2⁡30 )=3.27 m/s^2
The acceleration am is:
a_m=a/cos⁡θ =3.27/cos⁡30 =3.78 m/s^2
And the tension T is:
T=ma/cos^2⁡θ =(3∙3.27)/cos^2⁡30 =13.8 N

If we consider the friction, then we get from equations 1) and 2):

Acceleration of mass M:
a=9.8 (4(cos⁡25+0.3 sin25)- 3*0.3)/(3⁄cos⁡25 +4(cos⁡25+0.3 sin25) )=4.26
Acceleration of mass m:
a_m=a/cos⁡θ =4.26/cos⁡25 =4.7 m/s^2
Tension in the cable is:
T=m/cosθ ((a+ g cosθμ)/(cos⁡θ+sinθμ))=3/cos⁡25 ((4.26+0.3∙9.8∙cos⁡25)/(cos⁡25+0.3 sin⁡25 ))=22.18 N
Relative motion of masses - example 16 Print example 16 ▲
Relative motion example 16
Free body diagram
m1 kg
m2 kg
m3 deg
a1
m/s2
a2
m/s2
a3
m/s2
T1
N
T2
N
Acceleration directions
m1 m2 m3
Find the acceleration of the system of masses neglecting the mass of the string and the mass of the pulley.
We assume arbitrary that all three accelerations are downward and are equal to a1 a2 and a3 . Now we can write the forces acting on each mass as:
ΣFy on mass  m1 m1 g − T1 = m1 a1 (1)
ΣFy on mass  m2 m2 g − T2 = m2 a2 (2)
ΣFy on mass  m3: m3 g − T2 = m3 a3 (3)
ΣFy on pulley B: T1 = 2 T2 (4)
We can see that we have 5 unknowns and only 4 equations so we have to derive another equation from the accelerations, a1 is equal to the acceleration of pulley B which should be half the accelerations of a2 and a3 but in negative sign because when a1 is going down pulley B is going up, but we chose the accelerations in the downward direction.
Σ Accelerations: a1 = −(a2 + a3) / 2 (5)
a3 = − 2a1 − a2
The minus sign is because a1 is in the opposite direction to a2 and a3. Substitute the value of T1 from eq. (4) and a3 from eq. (5) to eq. (1) (2) and (3) to get the matrix form:
Friction example 1
Solving by Cramer's rule we have:
D = 2 (m2m3 + m2m3) + m1(m3 + m2) = m1m2 + m1m3 + 4m2m3
Friction example 1
Friction example 1
Friction example 1
Friction example 1
After division of the numerator and the denominator by m1m2m3 we got another form for T2 Friction example 1
If all masses are the same and equal to M then:
Friction example 1 Friction example 1
Friction example 1 T2 = 2 g M / 3
Friction of two masses example - 17 Print example 17 ▲
Example 17 Free body diagram of m1 Free body diagram of m2 Free body diagram of m3
from the forces diagram we can write the equilibrium equations:
On mass m1 ΣFx = T1 = f1 = m1 g μ1 (1)
On mass m2 ΣFx = T2 − f1 − f2 = m2 a
           T2 − m1 g μ1 − (m1 + m2) μ2 g = m2 a (2)
On mass m3 ΣFy = m3 g − T2 = m3 a (3)
Acceleration of m2 and m3 (4)
From eq. (3)   T2 can be found T2 = m3(g − a)  = Tension T2
Q: Given three masses  m1  equal to  m,  mass  m2  equal to  3m  and  m3  equal to  2m,  μ1 = 0  and masses  m2  and  m3  are moving at a constant velocity. Find the value of  μ2,  T1  and  T2
S:
For steady velocity we need that a = 0
From the acceleration equation (4) we have:     m3 − m1 μ2 − m2 μ2 = 0
Friction coefficient example 17
Because there is no friction between surfaces of masses m1 and m2 then:       T1 = 0
Because the acceleration is 0 the tension T2 in cable m3 is:       T2 = m3 g
Friction of two masses example - 21 Print example 21 ▲
Three masses and pulleys example 21 Free body diagram m1 Free body diagram m2 Free body diagram m3
Three masses are hanging on frictionless pulleys as shown in the figure. Find the acceleration of the masses.
We choose arbitrary the direction of the accelerations of masses m1 and mass m2 as upward and the acceleration of m2 downward.
From the forces diagram on the masses, we have.
On mass  m1 ΣFy = T − m1 g = m1 a1 (1)
On mass  m2: ΣFy = m2 g − 2T = m2 a2 (2)
On mass  m3: ΣFy = T − m3 g = m3 a3 (3)
From accelerations: Friction example 1 (4)
Note: when mass  m1  is moving  x1  distance upward and mass  m3  a distance of  x3  upward, the contribution to the displacement of mass m2 is the sum of half of this displacements  x2 = (x1 + x3) / 2  in the downward direction.
The equations with the unknowns T, a1, a2 and a3 can be solved by Cramer's rule or by direct substitution.
Write the equations in the matrix form Friction example 1
D = − m2m3 − 4m1m3 − m1m2 = − (m1m2 + m2m3 + 4m1m3)
Friction example 1
Friction example 1
Friction example 1
Friction example 1
Find the acceleration and the tension in the rope if all the masses are equal to   m1 = m2 = m3 = m
T = 2 m g / 3a1 = − g / 3a2 = − g / 3a3 = − g / 3    T = 2 m / 3
Notice that if     m1 = m3 = m     and     m2 = 2m     then the accelerations will be 0  and     T = m
If the result of the acceleration is negative then the motion is opposite to that chosen.
Friction of two masses example - 24 Print example 24 ▲
Friction example 24
Free body diagram of mass m1
Free body diagram of mass m2 and m3
Free body diagram of mass m1
 Three masses are connected with a rope of 0 mass as shown in the figure, a force  F  is apply to mass  m3 , friction coefficient  μ  if present between mass  m1  and the surface that is tilted by θ deg. Find the value of the force F that will keep the system at rest, if the force F is cancelled find the acceleration of the system.
To determine the direction of the motion we have to analyse the relationship of the equations:
m3 > m2 + m1 sinθ Motion is m3 down (a)
m3 < m2 + m1 sinθ Motion is m3 up (b)
m3 = m2 + m1 sinθ No motion (c)
Assume that the acceleration of mass m3 is downward then:
On mass  m1 ΣFx = T1 − μ m1 g cos θ − m1 g sinθ = m1 a (1)
On mass  m2 ΣFy = T2 − m2 g − T1 = m2 a (2)
On mass  m3 ΣFy = m3 g + F − T2 = m3 a (3)
The same equations when the acceleration is to the left are:
On mass  m1 ΣFx = m1 g sinθ − T1 − μ m1 g cosθ = m1 a (4)
On mass  m2 ΣFy = m2 g + T1 − T2 = m2 a (5)
On mass  m3 ΣFy = T2 − m3 g − F = m3 a (6)
We got three equations with three unknowns   T1   T2   and   a.
Solving eq. (1) (2) and (3) according to Cramer's rule we get:
Value of acceleration
Tension T1
Tension T2
Solving eq. (4) (5) and (6) according to Cramer's rule we get:
Value of acceleration
Tension T1
Tension T2
The minimum force  F  needed to apply when a = 0, when the motion is intended to be to the left is:
F = g ( m1 sinθ + m2 − m3 ) − m1μs g cosθ
The maximum force  F  needed to apply when a = 0, when the motion is intended to be to the right is:
F = g ( m1 sinθ + m2 − m3 ) + m1μs g cosθ
In the case when F = 0 mass m3 that keeps the system at rest is in the range of:
m1 ( sinθ − μ cosθ ) + m2   <   m3   <   m1 ( sinθ + μ cosθ ) + m2
If all three masses are of the same weight  M  then the force  F  at rest should be in the range:
M g (sinθ − μs cosθ)   <   F   <   M g (sinθ + μs cosθ)
Friction of two masses example - 33 Print example 33 ▲
Three masses are connected to each other by ropes of 0 mass, a force F is applied to mass m3. Find the value of the tension in the ropes and the acceleration of the masses if a friction coefficient of μ exists between the masses and the surface. Three masses example 33
Free body diagram m1 Free body diagram m2 Free body diagram m3
From the free body diagram, the friction forces and the equilibrium equations of the masses are:
Friction forces: f1 = m1 g μ f2 = m2 g μ f3 = m3 g μ
ΣFx = T1 − m1 g μ = m1 a (1)
ΣFx = T2 − T1 − m2 g μ = m2 a (2)
ΣFx = F − T2 − m3 g μ = m3 a (3)
We got three equations with three unknowns T1 T2 and a
Friction example 1
According to Cramer's rule the value of the coefficient’s determinant is   D = − (m1 + m2 + m3)
Friction example 1
Friction example 1
Friction example 1
Another way to solve the problem is to look on the three masses as one mass equal to  M = m1 + m2 + m3
Friction example 1 From the free body diagram, we have: F − M g μ = M a and a is:
Friction example 1
Once we found the acceleration  a  we can use eq.  (1)  and  (2)  to find  T1  and  T2 
Friction of two masses example - 37 Print example 37 ▲
Pulley example 37 Free body diagram mass m1 Free body diagram mass m2 Free body diagram of the pulley
Two masses  m1  and  m2  are located on the floor the masses then connected by a pulley as shown in the figure. Find the acceleration of the masses and the tension in the rope connecting the masses if a force of  F  is apply to the pulley upward, suppose that  m1 > m2.
We mark the accelerations of the masses as  a1  and  a2,  from the free body diagram we get:
On mass  m1: ΣFy = T − m1 g = m1 a1 (1)
On mass  m2: ΣFy = T − m2 g = m2 a2 (2)
On the pulley: ΣFy = F = 2 T (3)
From eq. (3) we get: T = F / 2
And substituting T to eq. (1) and (2) we get: Acceleration a1 Acceleration a2
Notes:  because accelerations a1 and a2 can not be negative (opposite to the direction shown) because of the floor there are some unique cases:
Small mass m2 Samll mass m2 F < 2 m2 g The force F is not enough to lift any one of the masses
Bigger mass m1 Bigger mass m1 2 m2 g < F < 2 m1 g The force F will lift the small mass but not the bigger mass
F will lift both masses 2 m1 g < F The force F will lift both masses
For example, if mass m1 = 30 kg and m2 = 20 kg then find the accelerations when F = 100N, F = 400N and F = 1000N.
F [N] a1 [m/s2] a2 [m/s2] Notes
100N 100 / 30 − 9.8 = − 6.5 100 / 20 − 9.8 = − 4.8 No lift of any mass   a1 = 0   a2 = 0
200N 200 / 30 − 9.8 = − 3.1 200 / 20 − 9.8 = 0.2 Only small mass is lifted   a1 = 0
1000N 400 / 30 − 9.8 = 3.5 400 / 20 − 9.8 = 10.2 Both masses move upward
Friction of two masses a force and pulley - example 38 Print example 38 ▲
Friction example 38
Free body diagram
m1 kg
m2 kg
μ
F N
θ deg
a m/s2
T
N
f
N
Mass m1 and m2 are at rest when a force F is applied at an angle of θ degree. Find the maximum force F that the system will stay at rest and the acceleration of the system.
The friction force acting on  m1  is:     f = N μ = (m1 g + F sin θ) μ.
To determine the possible direction of the motion we have to check the forces acting on mass m1 without friction force.
if     F cosθ > m2 g m1 moves to the left (a)
if     F cosθ < m2 g m1 moves to the right (b)
After we determined the direction of the motion, we can set the right direction of the friction force and check if there is motion at all due to the friction force.
Let assume that the acceleration of m1 is to the left, from the free body diagram we have
assume
On m1 F cosθ − f − T = m1 a (1)
On m2 T − m2 g = m2 a (2)
From eq. (1) and (2) we can find the values of a and T
If we assume that the acceleration of mass m1 is to the right direction the equilibrium equations will be as follows:
On m1 T − F cosθ − f = m1 a (3)
On m2 m2 g − T = m2 a (4)
If we get a negative value for the acceleration in both directions then motion is not possible.
The conditions for motion are:
If F cosθ − f > m2 g m1 moves to the left (c)
If F cosθ + f < m2 g m1 moves to the right (d)
The range of the force F that the system is at rest is when it is equal to the friction force in both directions:
Friction example 1
the static and dynamic friction coefficient between the surface and  m1  is  μ = 0.4.  Find the friction force acting on  m1  if the force equal  250N  and  θ = 30  degree and  m1 = 10kg  and  m2 = 30 kg.
First, we check conditions (c) and (d) to verify if the masses are moving.
Condition (c) 30 * g > 250 * cos30 + (10 * g + 250 * sin30) 0.4 False
Condition (d) 30 * g < 250 * cos30 - (10 * g + 250 * sin30) 0.4 False
Because both conditions are false the system is at rest.
a) Friction force can not be calculated by the equation for  f  because there is no movement, f  will be calculated by the difference between force of mass    m2 g   and   F * cosθ
f = m2 g − F * cosθ = 30 * 9.8 − 250 * cos30 = 77.5 N
b) maximum force F F = g(10*0.4 + 30) /(cos 30 - sin 30 * 0.4) = 500.3 N
c) acceleration when F = 0 a = −g(10*0.4 - 30) /(10 + 30) = 6.4 m / s2
Two masses and two pulleys example - 40 Print example 40 ▲
Friction and pulley - example 40 Free body diagram m1 Free body diagram m2
Two masses m1 and m2 are connected through 2 pulleys as shown in the figure the friction of m1 and the surface is μ. Find the accelerations and the tensions in the ropes.
In order to find the direction of the motion we will analyse the forces on the pulley by neglecting the friction force, it is easy to see that if:
m1 sinθ > 2 m2 m1 is moving downward (a)
m1 sinθ < 2 m2 m1 is moving upward (b)
m1 sinθ = 2 m2 There will be no motion (c)
If m2 exceeds a maximum value then mass m2 will start to move down and the friction force direction will be as shown in the free body diagram at right.
The friction force is equal to: f = N1 μ = m1 g cosθ μ
From the forces diagram on mass  m1  and  m2  and assuming that the acceleration is to the downward direction of mass m2 we have.
On mass  m1 ΣFx = T1 − f − m1 g sinθ = m1 a1 (1)
On mass  m2: ΣFy = m2 g − T2 = m2 a2 (2)
From the accelerations: a2 = 2a1 (3)
From the pulley tension: T1 = 2T2 (4)
Solving for a1 and T2 we get:
Acceleration
Tension
If we solve the case that m1 accelerates downward then the forces equations will be:
On mass  m1 ΣFx = m1 g sinθ − T1 − f = m1 a1 (5)
On mass  m2: ΣFy = T2 − m2 g = m2 a2 (6)
Eq. (3) and (4) are the same in both cases, solving the equations we get:
Acceleration
Tension
The range of m2 that the system will stay at rest is (in this case the accelerations a1 are equal to 0):
m2 range