☖ Home ⇄ Units Converter ⧉ Geometry Σ Math ✈ Physics 〶 Electricity

Rotational motion solved problems

Notes about calculating rotational motion

Print notes
When dealing with circular motion there are some parameters that we should be familiar with.
T Time of 1 cycle Friction example 1 s
f frequency Friction example 1 Hz
ω angular velocity Friction example 1 rad / sec
α angular acceleration Friction example 1 rad / sec2
v tangential velocity Friction example 1 m / s
aR radial acceleration Friction example 1 m / s2
FR Centripetal force Friction example 1 N
r radius of motion r m
If angular velocity is given in (rpm) then     ω = (rpm) 2π / 60   [rad / s]
Forces conversion:     1  [kgf] = 9.8  [N] = 9.8  [kgm · m / s2]
Rotational motion example - 1 Print example ▲
Rotation around bar Rotation free body diagram Rotation free body diagram
Find the angle  α  if the mass  m  is rotating at an angular velocity of  ω  around the vertical rode, the rope length is  L.
From centrifugal force equation we have: T sinα − m ω2 R = 0 (1)
From forces equilibrium in the y direction: T cosα − m g = 0 (2)
We have also the equation: R = L sinα (3)
Substitute (1) into (2) to get the value of angle α Tan rotation angle Rotation angle
If we substitute equation (3) into (1) and (2) we get: Cos rotation angle Rotation angle
From the equation above we notice that the angle α is not a function of the mass m.
The height of the pendulum is     h = L cosα     if we substitute the value of  cosα  we get:       h = g / ω2
The tension in the chord is calculated by eq.  (1)  and  (3) : T = m ω2 L
Rotational motion example - 2 Print example ▲
Vertical circular motion Vertical motion free body diagram
The mass  m  is turning vertically at a constant angular velocity of  ω rad/s  if the rope length is  R, find the tension in the rope at points  A, B  and  C.
From the forces diagram we can write the total forces acting in the radial (to the center):
In the R direction: T + m g sinα − m ω2 R = 0 (1)
And the tension T is T = m ω2 R − m g sinα
And the tension at the points A, B and C are found by inserting the angles into the expression for T.
At point  A  (α = − 90 °) T = m (ω2 R + g)
At point  C  (α = 90 °) T = m (ω2 R − g)
At point  B T = m (ω2 R − g sinα)
We can see that the tension in the rope is minimum at point  C  and maximum at point  A,  and between this points  T  is a function of the angle α .
At the top the tension in the rope has its minimum value therefore in order to keep the mass not to fall the angular velocity should be at least:
m ω2 R = m g → angular velocity so, the angular velocity should be: Minimum angular velocity
If we substitute the velocity   v = ω R ,   we obtained the minimum speed: Minimum velocity
Rotational motion example - 3 Print example ▲
Pendulum swirl around nail Pendulum swirl data Pendulum swirl free body diagram
The mass  m  is released from rest at point  A. When the mass reaches vertical position, the rope turns around a nail which is located at a distance of  r  from the end of the rope. Find the angle  α  that will cause a complete rotation of the mass around the nail.
We will take the axes so that the x direction is pointing to the center of the rotation and the y direction is always tangential to the circle in this axes system the equations are simpler:
The velocity of the mass at the vertical position when the rope reaches the nail is calculated by energy methods.
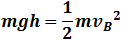The initial potential energy is converted to kinetic energy: Potantial and kinetic energy balance
Falling distance is: h = R − R cosα = R (1 − cosα)
The velocity at point B is: 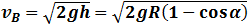Velocity at lower point (1)
In order to complete a hole rotation around the nail the kinetic energy at point B (vertical position) should be equal to the potential energy at height 2r (upper position of the mass after swirling around the nail) plus the kinetic energy at top due to the velocity vT .
Energy balance: 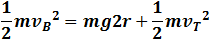Energy balance (2)
From free body diagram 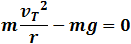Vertical forces equilibrium (3)
From eq. (3) vT2 = g r (4)
Substitute eq. (1) and (4) into (2) we get: m 2 g h / 2 = m g 2 r + m g r / 2
h = 5 r / 2
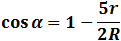Substitute the value of  h  to the previous found value of  h  we get: angle cos
If point  A  is horizontally located relative to point  O  and the ball released from this position, find the maximum value of  r  that will cause a complete rotation around the nail.
In this case:       h = R       and from eq. (1)       vB2 = 2 g R       substitute this value into eq. (2) we get:
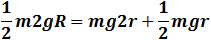Energy balance case h = R
And finally:r = 2 R / 5
Pendulum on cart example - 4 Print example ▲
Pendulum on a cart Free body diagram
A pendulum is tilted to an angle  θ  due to horizontal acceleration  a [m / s2] of the cart, the mass of the pendulum is  m, find the angle  θ  and the tension in the cord expressed by the mass and acceleration.
From the free body diagram, the forces equilibrium in x and y direction are:
x direction: T sinθ = m a (1)
y direction: T cosθ = m g (2)
By dividing eq. (1) with eq. (2) we can find the angle θ : Tilt angle (3)
From equation  (3)  we see that the tilt angle is a function of the acceleration  a  and the gravitational acceleration  g.
The tension in the rope can also be eliminated: Tension or Tension
Rotationsl motion example - 5 Print example ▲
Bullet colision A bullet is shoot into a block of wood suspended from a light flexible wire. The bullet lodges in the wood and causes it to tilt to an angle  θ. Find the angle  θ  as a function of  m,  M,  L,  v1  and  v2 .
Note: We suppose that the impact is ideal and there are no heat and plastic loose.
After impact the velocity of the bullet and wood are the same, from conservation of momentum we have:
m v1 = (m + M) v2 (1)
From conservation of energy: 1/2 (m + M) v22 = (m + M) g L cosθ (2)
From equation (2) eliminating θ we get: Angle of reaction
From eq. (1) we have: Velocities values
If we have to find  v1  then from the equations  (1) we have: Final velocity
And v1 is: Initial valocity (3)
For example, if a bullet mass is 10 gram and the wood mass is 1 kg. After the collision it is observed that the wood mass center is 20 cm above the original height. Find the velocity of the bullet before impact.
From eq. (3) we have: Numeric initial valocity
Rotational motion example - 6 Print example ▲
Centrifugal valve
Motion free body diagram
Two spheres each with mass m, are connected by four ropes of length  L  as shown in the figure, both masses are connected to a mass M that can move freely up and down the rode. The system is rotating at an angular velocity ω rad / s. Find the angle θ as a function of m, M, L and ω.
Note:   If the weight W is given in kg then   m = W / g   [kgm]
From forces equilibrium equations of the spheres, we have:
x direction F1 cosα + F2 cosα − m r ω2 = 0 (1)
y direction F1 sinα − F2 sinα − m g = 0 (2)
From forces equilibrium equation of the mass M in y direction.
2F2 cosθ − M g = 0 (3)
Now we substitute the values: r = L sinθ       and       α = 90 − θ
From eq. (1) we get: F1 + F2 = m L ω2
From eq. (2) we get: Tension balance
Solving the above equations for F1   and   F2   we get:
Tension T1 Tension T2
Substitute  F2  into  (3)  we get:
Angle function → Angle value
Find the angular velocity if the angle θ is given:
From eq. (3) we have: Tension F2
Inserting this value to the value of F2 we get: Angular velocity
Motorist turn example - 7 Print example ▲
Motorist turn
Motorist free body diagram Motorist free body diagram
A motorist is driving at a velocity of  v [m / s], he is performing a turn of a radius  r. Find the angle  θ  that the motorcycle should be during the turn, and the minimum friction required in order to prevent the slipping of the motorcycle.
During the turn the centrifugal force is balanced by the weight of the motorcycle, from equilibrium of forces we get:
x direction: m ω2 r − f = 0 (1)
y direction: N − m g = 0 (2)
Moments at point A: m g sinθ L − m ω2 r cosθ L = 0 (3)
The value  L  is the distance of the center of mass to the wheel end (point A), but  L  has no effect on the calculations because after dividing eq. (3) by  L  it disappears.
From eq. (3) we can find the tilt angle θ :
Turn angle tan → Turn angle
The friction force is: f = μs N   this force is balanced by the centripetal force.
Substitute the value of f into eq. (1) and (2) we get:
Turn angle tan (4)
In order not to slip the friction coefficient should be bigger than the value calculated:
Rotational motion example - 8 Print example ▲
Motion around circle
Free body diagram
A small ball is in rest at point  A. the ball is then slipping down on a circular path of radius  R. Find the height  h  of the point B where the ball separates from the circular path.
Note:   we suppose that the radius of the ball is much less then the radius of the circular path and there is no friction during the motion.
When separation begins the increasing centrifugal force due to gravitational acceleration  g  is balanced by the value of   mg cosθ. We choose the  y  axis pointing to the center of the circle path.
Forces equilibrium → Forces equilibrium (1)
In order to find the velocity at  B  we use energy method.
Energy balance → velocity of ball (2)
The value of h expressed by  R  is: h = R − R cosθ = R (1 − cosθ)
Angle of separation (3)
Substitute (2) and (3) into eq. (1) to get the separation height: Separation height (4)
And the speed at separation point is: Separation velocity
Separation angle from eq. (3) is: Separation velocity
Rotational motion example - 9 Print example ▲
Circular motion Free body diagram
A small ball is released from rest at point  A, at point  B  it enters a circular tube of radius  r. Find the height  h  that the ball should be released in order to reach point  C, what is the velocity of the ball at point  C  suppose that the friction is negligible.
At point C the minimum velocity should be:
Forces equilibrium → Velocity at point Vc (1)
The energy of the ball at points  B  compared to  C  is:
Energy equilibrium → Velocity at point Vb (2)
Now we can compare the energy of the ball at points  A  and  B.
Energy at A and B (3)
Isolating h and substitute equation (2) into eq. (3) we get the released height:
Release height (4)
If high h is equal to  4r  what is the force of the ball on the circles surface at points B and C.
From energy balance at points A and B we have: Release height
The reaction force at point B is: Release height
The velocity at point C from energy: Release height
The reaction force at point C is: Release height
Rotational motion example - 10 Print example ▲
Motion along a rod Free body diagram
A circular tube is rotating around the vertical axis at a fixed angle of  θ  degree and an angular velocity  ω [rad / s]. Inside the frictionless tube a ball is released, if the mass of the ball is  m, determine the radius  r  that the ball will reach.
We choose the  x-y  axis to coincide with the tube axis. The forces along  y  axis that causes the ball
to be at equilibrium are: m r ω2 sinθ = m g cosθ (1)
Isolate  r  from equation (1) we get: Balance radius
Motion along a rod Motion along a rod
If friction coefficient between the mass and tube wall is μs and the mass is located at a distance r from the rode find the range of the angular velocity that will keep the mass at rest.
To find the maximum angular velocity the direction of the mass is upward and the friction force is downward.
Forces in x direction: N = m ω2 r cosθ + m g sinθ (1)
Forces in y direction: m g cosθ + f = m ω2 r sinθ (2)
The friction force is         f = N μs
Maximum angular velocity is: Balance radius
To find the minimum angular velocity the direction of the mass is downward hence friction force is upward.
Forces in x direction: N = m ω2 r cosθ + m g sinθ (3)
Forces in y direction: m g cosθ − f = m ω2 r sinθ (4)
Minimum angular velocity is: Balance radius
Road banking example - 11 Print example ▲
Car turn Free body diagram
v
m/s
θ
deg
R
m
μ
M
kgm
f
N
N
N
Input:
Icy road friction  μs = 0
Balance radius
Balance radius
Balance radius
Flat road   θ = 0
Balance radius
Balance radius
Balance radius
A car is traveling at a speed of  v m/s  when it enters a turn of radius  R  the friction of the wheels with the road is  μs  in order to prevent skidding of the car the road is banked by an angle of  θ degree. Find the maximum speed with no skidding of the car.
The maximum friction force of the car is:             f = N μs
For present solution we neglect the moment caused by the friction of the wheels compared to the center of the car mass.
The axes is chose so that the x is along the road surface to the center and y is normal to the road surface.
Forces along x axis: Balance radius (1)
Forces along y axis: Balance radius (2)
Isolate  v  from eq. (1) and (2) we get: Turn maximum speed
If we need to find the banking angle then from eq. (1) and (2) we have:
Turn maximum speed
Note that the velocity v and banking angle is not a function of the mass.
If   Rgμs   is bigger then   v2   then the angle is negative that means that no banking of the road is needed.
from (1) and (2) μs is: Turn maximum speed
Radius of road curvature: Turn maximum speed