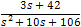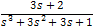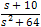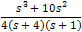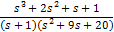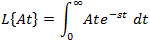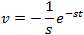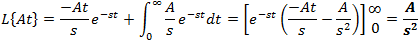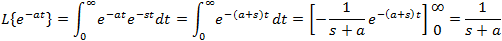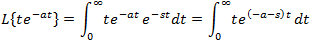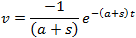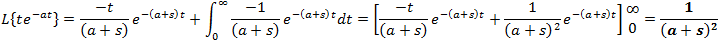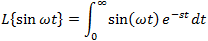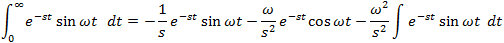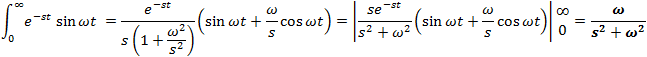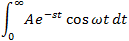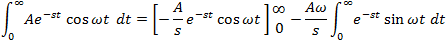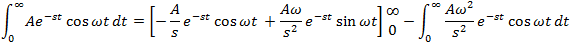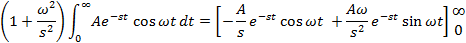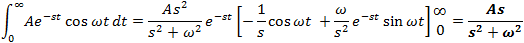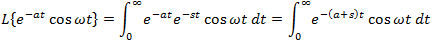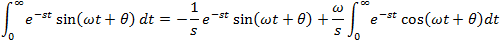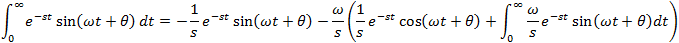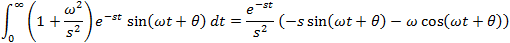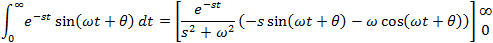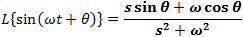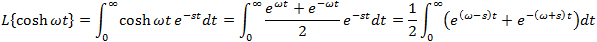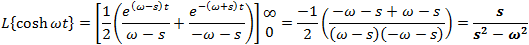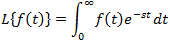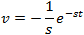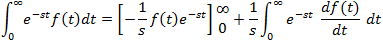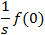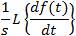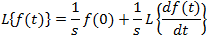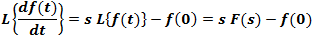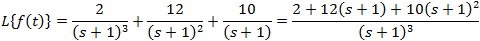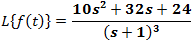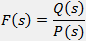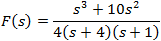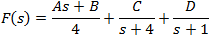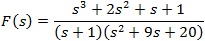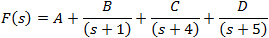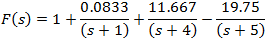Taylor and Maclaurin series

Laplace Transform

If f(t) is a function of t, defined for all t > 0, the Laplace transform of f(t), denote by the symbol
L{ f (t) } is defined by: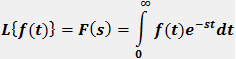

where s may be real or complex. In circuit applications we assume s = σ + jω. The operation L{f(t)} transforms a function f(t) in the time domain into a function F(s) in the complex frequency domain or simply the s domain.

Laplace tables

Solved examples:

At e^−at te^−at sin ωt Acosωt e^−atcosωt sin(ωt + θ) cosh ωt df(t) / dt e^−t(t² + 12t + 10)

Solved problems of Laplace transform

Example 1a: Obtain the Laplace transform of f(t) = At where A is a constant.

The Laplace trensform is defined by the integral:

Apply integration by parts:	u = At	→	du = A dt
	dv = e^−st dt	→

Example 2a: Obtain the Laplace transform of f(t) = e^−at where a is a constant.

Example 3a: Obtain the Laplace transform of f(t) = te^−at where a is a constant.

The Laplace trensform is defined by the integral:

Apply integration by parts:	u = t	→	du = dt
	dv = e^{− (a + s)t} dt	→

Example 4a: Find the Laplace transform of f(t) = sin(ωt)

The Laplace trensform is defined by the integral:

Apply integration by parts:	u = sin ω dt	→	du = ω cos ωt dt
	dv = e^−st dt	→

Apply integration by parts second time on the cos term on the right side of the integral:

u = cos ω dt	→	du = −ω sin ωt dt
dv = e^−st dt	→

Example 5a: Find the Laplace transform of f(t) = A cos ωt

The Laplace trensform is defined by the integral:

Apply integration by parts:	u = A cos ωt	→	du = − Aω sin ωt dt
	dv = e^−st dt	→

Apply integration by parts second time on the cos term on the right side of the integral:

u = sin ωt	→	du = ω cos ωt dt
dv = e^−st dt	→

Example 6a: Find the Laplace transform of f(t) = e^−at cos ωt

The Laplace trensform is defined by the integral:

Apply integration by parts:	u = e^{−(s + a)t}	→	du = −(s + a)e^{−(s + a)t} dt
	dv = cos ωt dt	→

u = e^{−(s + a)t}	→	du = −(s + a)e^{−(s + a)t} dt
dv = sin ωt dt	→

The integrals on both sides of the equation are the same and can be added.

Example 7a: Find the Laplace transform of f(t) = sin (ωt + θ)

The Laplace trensform is defined by the integral:

Apply integration by parts:	u = sin (ωt + θ)	→	du = ω cos (ωt + θ) dt
	dv = e^−st dt	→

Apply integration by parts second time on the integral at the right side to get:

u = cos (ωt + θ)	→	du = ω sin (ωt + θ) dt
dv = e^−st dt	→

And finally:

Example 8a: Find the Laplace transform of f(t) = cosh ωt

The Laplace trensform is defined by the integral:

The second term reach zero at infinity, the first term is zero only when s>|ω|

Example 9a: Find the Laplace transform of the derivative of f^'(t) = df(t) / dt.

The transform of f(t) is:

(1)

From integration by parts:

Set:

u = f(t)thendu = df(t)

dv = e^(-st) dtthen Integration by parts

Performing the integration:

First term is:

Second term is:

Equation (1) get the form:

Evaluating derivation:

Example 10a: Find the Laplace transform of: f(t) = e^−t (t² + 12t + 10)

Open parenthesis we get:

L{f(t)} = e^−t t² + 12e^−t t + 10e^−t

According to the transforms table,find the transformation of each term.

Solved problems of inverse Laplace transform

Example 1b: Find the inverse Laplace transform of the function:

Rearanging terms:
From table:	L^-1 [F(s)] = 3e^{− 5t} cos 9t + 3e^{− 5t} sin 9t = 3e^{− 5t} (cos 9t + sin 9t)

Example 2b: Find the inverse Laplace transform of the function:

Rearanging terms:
From table:

Example 3b: Find the inverse Laplace transform of the function:

Rewrite the polinomials as:
After aranging terms:

Laplace transform by partial fraction technique.

If Q(s) and P(s) are polinomials and		then the inverse Laplace can be found by
the partial fraction technique (see next examples).

Example 4b: Find the inverse Laplace transform by using the partial fraction method of the function

Rewrite the polinomials as:

After aranging terms we get the following form:

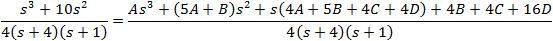By comparing the coefficients we get the following set of linear equations:

A = 1

5A + B = 10

4A + 5B + 4C + 4D = 0

4B + 4C + 16D = 0

Solving the set of linear equations we get: A = 1, B = 5, C =− 8, D = 0.75

From the tables we get:

F(t) = 0.25u(t) + 1.25δ(t) − 8e^{− 4t} + 0.75e^−t

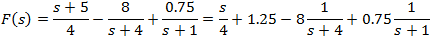
Example 5b: Find the inverse Laplace transform by partial fraction method of the function:

Find the denominator roots (also called poles) and rewrite the polinomials as followes:

(A,B,C and D are to be determined)

s³ + 2s² + s + 1 = A(s³ + 10s² + 29s + 20) + B(s + 4)(s + 5) + C(s + 1)(s + 5) + D(s + 1)(s + 4)

After arranging the powers of s we get the values:

s³ + 2s² + s + 1 = (A)s³ + (10A + B + C + D)s² + (29A + 9B + 6C + 5D)s + (20A + 20B + 5C + 4D)

The coefficients of s in the right and left side of the equation must be the same, now we have to solve the system of linear equations of 4 unknowns:

1 = A

2 = 10A + B + C + D

1 = 29A +9B + 6C + 5D

1 = 20A + 20B + 5C + 4D

And the solutions of the coefficients are: A = 1 B = 0.0833 C = 11.667 D = − 19.75

F(s) can be written as:

The inverse Laplace transform is:

L^{− 1} [F(s)] = δ(t) + 0.0833e^−t + 11.667e^{− 4t} − 19.75e^{− 5t}

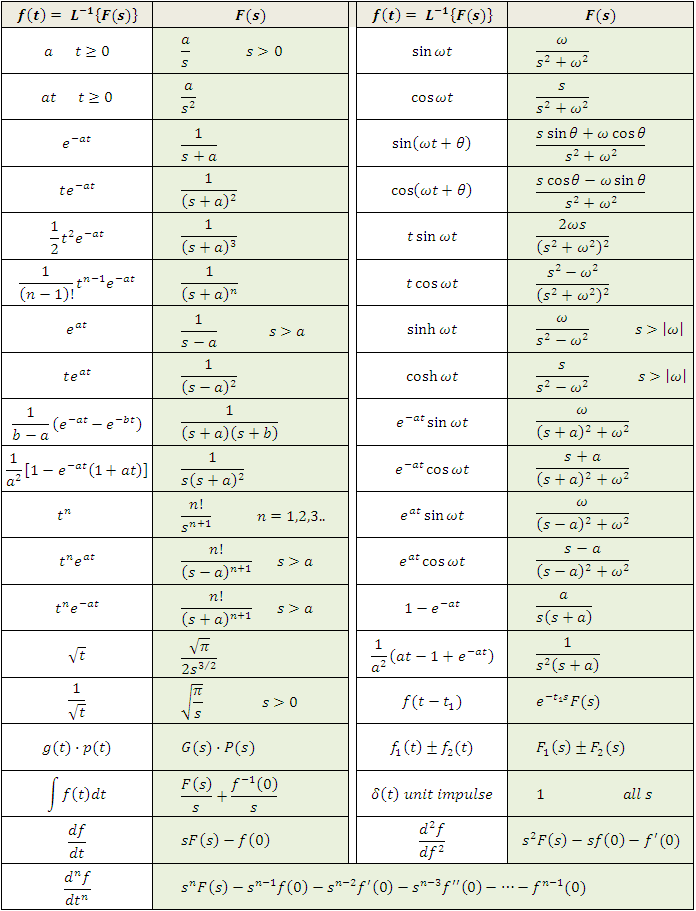
Laplace transform tables