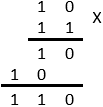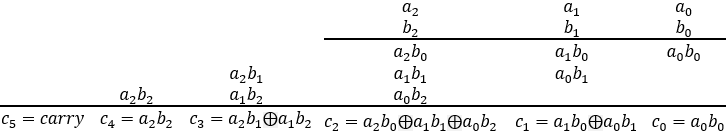⇄ Units Converter ⧉ Geometry Σ Math ✈ Physics 〶 Electricity
2 bits multiplier example 1 Print 2 bits multiplier ▽ ▲
0
×
0
=
0
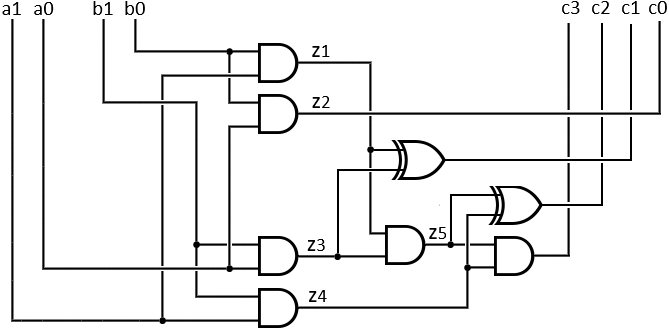
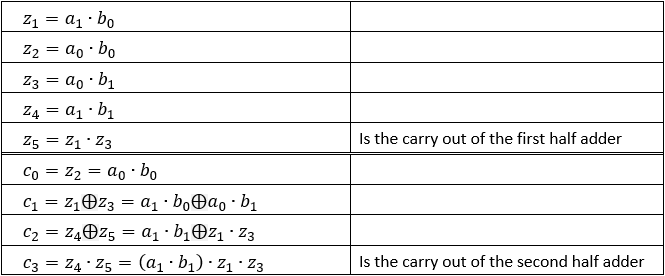
Sum output
Sum output
Let multiply two bits first bit is:  (1 0) and the second bit is:  (1 1) the result of this multiplication is: Multiplication example
The multiplication is made according to the following rules: Multiplication example Multiplication example

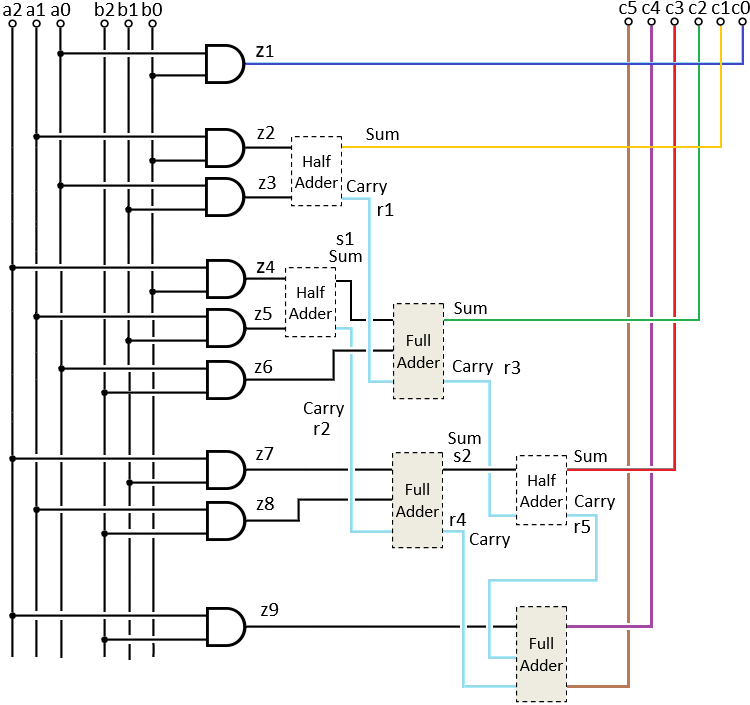
The general process of multiplying two sets of two bits (a1 a0) and (b1 b0) is according to the following steps: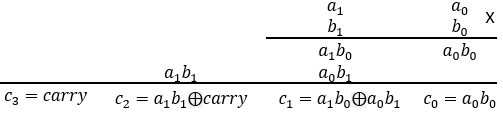

General 2 bits multiplication

In order to better understand the circuit of the set of two, two bits multiplier we draw the circuit with the half adder as a box, now we can see clearly way the calculations take place.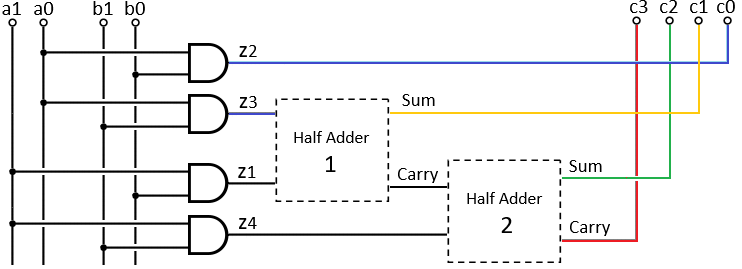

General 2 bits multiplication

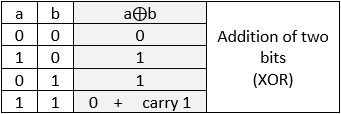
1) The result of the first multiplication is the value of c0 = a0b0 (blue line).

2) Now perform the addition of c1 = a1 b0 ⨁ a0 b1. This operation is performed by the half adder no. 1 circuit because it gets two values which are not including a carry from c0. (see example 12). The result sum is the value of c1 (yellow line).

3) Now perform the addition of c2 = a1 b1 ⨁ carry. This operation is performed by the half adder no. 2 circuit notice that one input is the result of the carry from half adder number 1. The sum is the value of c2 (green line).

4) The result of the carry of the second adder is the value of c3 (red line).

3 bits multiplier example 2 Print 3 bits multiplier example 2 △ ▲
×
=
General Half Adder

The half adder performs the addition of two bits by an XOR gate and return a carry with an AND gate.

The difference between Half Adder and Full Adder is the addition of an input carry to the Full Adder, (see example 12a). After calculation they both return the sum of two bits and a carry.

3 Bit Multiplier

While calculating values of c0 , c1, c3, c4 and c5 are straightforward, we have to explain about adding the term c2. Sometimes c2 should add 4 one's. we can see the results in the next table:

Addition case Result Decimal
0 + 0 0 0
1 + 0 1 1
1 + 0 1 1
1 + 1 10 2
1 + 1 + 1 11 3
1 + 1 + 1 + 1 100 4
1 + 1 + 1 + 1 + 1 101 5
1 + 1 + 1 + 1 + 1 + 1 110 6
1 + 1 + 1 + 1 + 1 + 1 + 1 111 7
1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 1000 8

The addition of 4 bits of one is giving a carry two places to the left (to c3 and c4 in this case), see the connection of the carry in the scheme.