Ellipse line intersection

Ellipse line intersection calculator

Ellipse equation

x² +

y² +

x +

y +

= 0

(x −	)²	+	( y −	)²	= 1

2			2

Line equation of the form mx + ny + c = 0

x +

y +

= 0

Intersection coordinates:
Notes and input limit

Ellipse and line intersection if h = 0 and k = 0
Ellipse and line intersection when x = 0 or y = 0
More examles of ellipse and line

Verify the equations of an ellipse and line intersection
Numeric example

Ellipse and line intersection when h ≠ 0 and k ≠ 0

Ellipse general equation is:

Line form:y = m x + c

The intersections x_1,2 coordinates are:

x_(1,2)=(b^2 h-a^2 mφ±ab√(b^2+a^2 m^2-2mφh-φ^2-m^2 h^2 ))/(b^2+a^2 m^2 )

The intersection x_1,2 coordinates are:

y_1,2 = m x_1,2 + c

Where: φ = c + k

Notice that when

a² m² + b² + 2hmφ − φ² − m² h² = 0

a² m² + b² − (c + k + hm)²

The line will be tangent to the ellipse

Ellipse and line intersection when h = 0 and k = 0 summary

Ellipse general equation is:

General form of an ellipse with center at (0 , 0)

Line form:y = m x + c

The intersections x_1,2 coordinates are:

x_1,2=(-a^2 mc±ab√(a^2 m^2+b^2-c^2 ))/(b^2+a^2 m^2 )

The intersection y_1,2 coordinates are:

y_1,2=(b^2 c±abm√(a^2 m^2+b^2-c^2 ))/(b^2+a^2 m^2 )

Or y_1,2 = m x_1,2 + c

Ellipse and line intersection if x = 0 or y = 0

ellipse form:

Line form: (vertical line)

x = d

x_1,2 = d

ellipse form:

Line form: (horizontal line)

y = d

y_1,2 = d

Verify the equations of an ellipse and line intersection

Find the intersection points of an ellipse and a line with center at (h, k)

The ellipse equation is given by:
		(1)
Line equation:	y = mx + c	(2)
The center of the ellipse is at (h , k)
Substitute eq. (2) into eq. (1)

Solving for x we have:

b²(x + h)² + a²(mx + φ)² − a²b² = 0	where φ = c + k
b²x² + 2hb²x + b²h² + a²m²x² + 2a²mφx + a²φ² − a²b² = 0
x²(b² + a²m²) + x(2a²mφ + 2hb²) + b²h² + a²φ² − a²b² = 0

The solution of this quadratic equation is:

x_1,2=(b^2 h+a^2 mφ±√((a^2 mφ-b^2 h)^2-(b^2+a^2 m^2 )(b^2 h^2+a^2 φ^2-a^2 b^2 ) ))/(b^2+a^2 m^2 )

x_1,2=(b^2 h-a^2 mε±√(a^4 m^2 ε^2-2a^2 mεb^2 h+b^4 h^2-b^4 h^2-b^2 a^2 ε^2+b^4 a^2-a^2 m^2 b^2 h^2-a^4 m^2 ε^2+a^4 m^2 b^2 ))/(b^2+a^2 m^2 )

Finally, we get:

(3)

Once the coordinate of x_1,2 are known we can find the y coordinates by substituting the v values into the equation of the line:

y₁ = m x₁ + c

y₂ = m x₂ + c

Numeric example of intersection between ellipse and line

Print numeric example of intersection of ellipse and line

Find the coordinates of the intersection of an ellipse given by the equation
and the line given by 2x − 4y − 5 = 0

From the equation of the ellipse, we can see that a < b so the ellipse is a vertical ellipse with vertices at:

the y axis at:	(h , k −b)	→	(2 , −3 − 6)	→	(2 , −9)
and	(h , k + b)	→	(2 , −3 + 6)	→	(2 , 3)

We have φ = c − k = −5/4 + 3 = 1.75 m = 0.5 a = 3 and b = 6

Solving equation (3) for x_1,2 we get:

x_1,2=(36∙2-9∙0.5∙1.75±3∙6√(36+9∙0.25-2∙0.5∙1.75∙2-〖1.75〗^2-〖0.5〗^2∙4))/(36+9∙〖0.5〗^2 )

x_1,2=(64.125±18√30.6875)/38.25=(64.125±99.713)/38.25=4.28 ,-0.93

From the equation of the line, we can get the y coordinates:

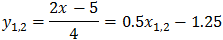y₁ = 0.5 · 4.28 − 1.25 = 0.89

y₂ = 0.5 · (−0.93) − 1.25 = −1.72

And the intersection coordinates are: (4.28 , 0.89) and (−0.93 , −1.72)

If we find the y coordinates according to equation (4) we get:

y_1,2=(36∙(-0.25)+9∙0.25∙(-3)±6∙3∙0.5√(36+9∙0.25+2∙(-0.25)(-3)-9-0.0625))/(36+9∙0.25)

y_1,2=(-15.75±9√30.6875)/38.25=(-15.75±49.86)/38.25=0.89 -1.72

Now we have to decide which y is the correct value for each x coordinate because the intersection point for example can be: (4.28 , 0.89) or (4.28 , −1.72) for that reason the better method to solve y coordinate is by using the value of y in the line equation as described before.

Now we have to check which pair of intersection point is located on the ellipse contour.

Check point (4.28 , −1.72)
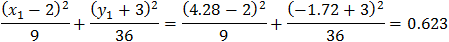Check point (4.28 , 0.89)

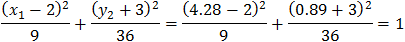We clearly see that the correct intersection point is: (4.28 , 0.89) and the second point is the remaining coordinates (−0.93 , −1.72)