Find if a point is inside an ellipse

Find if a point is inside or outside of an ellipse

Print if a point is inside or outside of an ellipse

Ellipse equation

x² +

y² +

x +

y +

= 0

( x −	)²	+	( y −	)²	= 1

2			2

Test point

Test point:	( , )
Point status:
Notes and input limit

Solved example

How to find if a point is inside or outside of an ellipse

ellipse form:

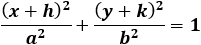Notice that the addition of the two fractions at the left side of the ellipse equation are equal to 1. now we have to check what happens if the addition of the two fractions is less then 1.

Instead of one we write the variable n

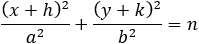
(x+h)^2/a^2 +(y+k)^2/b^2 =n

Define a value s so that the multiplication of s and n is equal to 1 so: s ‧ n = 1

The value of s should be:

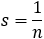Now divide the equation of the ellipse by n to get:

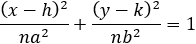Define new a_,² and b_,² these values are the new major and minor axes values, we see that

a_,² = na² and b_,² = nb²

We can easily see that the new major and minor values depend on the value of n, so when n is bigger then 1 the value of a_, and b_, are bigger, we can summarize the relations as follows:

n > 1

Point is outside the ellipse

n < 1

Point is inside the ellipse

n = 1

point is on the ellipse