|
We define two ellipses by the polynomial equations:
| Ax2 + By2 + Cx + Dy + E = 0 |
(1) |
| Fx2 + Gy2 + Hx + Iy + J = 0 |
(2) |
| From eq. (1) we get the value of y: |
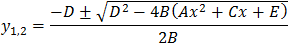 |
Substitute the value of y into equation (2) yields the equation:
After multiplying all terms by 4B2 and open paranthesis we get the equation
In order to simplepy the equation we will define the following constants:
| δ = |
2BDI − 2D2G + 4BEG − 4B2J |
| φ = |
4BCG − 4B2H |
| θ = |
4ABG − 4B2F |
| μ = |
2BI − 2DG |
| And we get the equation: |
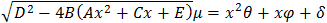 |
Taking the squares of bothe sides we get:
D2μ2 − 4ABμ2x2 − 4BCμ2x − 4BEμ2 = x4θ2 + x2φ2 + δ2 + 2θφx3 + 2θδx2 + 2φδx
After arranging the equation by powers we get a forthe power of x which can be solved mathematically:
x4θ2 + x32θφ + x2(φ2 + 2θδ + 4ABμ2) + x(4BCμ2 + 2φδ) + (δ2 − D2μ2 + 4BEμ2) = 0
|