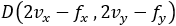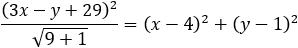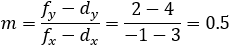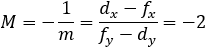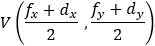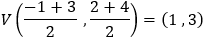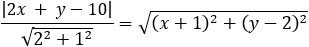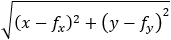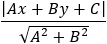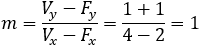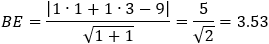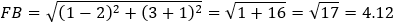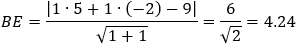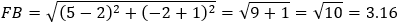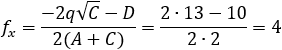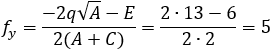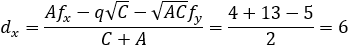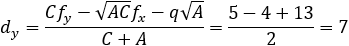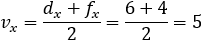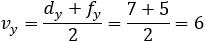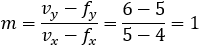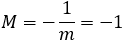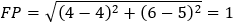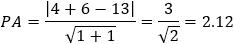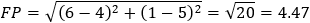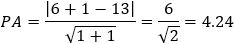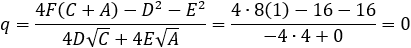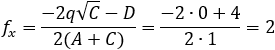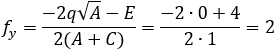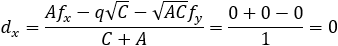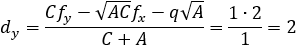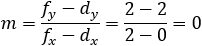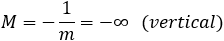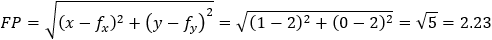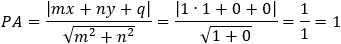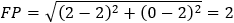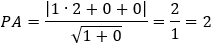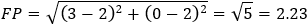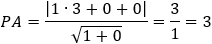|
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
|
Parabola and line intersection
|
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
|
Check if a point is inside of a parabola
|
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||
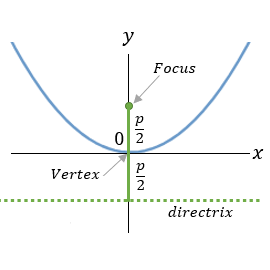
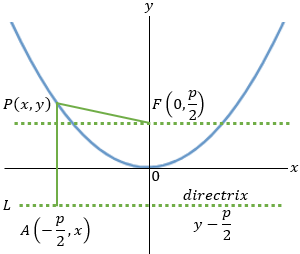
Notice that this parabola has the vertex at the origin and focus distance of p from the directrix.
If the vertex is located at (h , k) then the parabola equation becomes:
Notes:
|
|||||||||||||||||||||||||||||||||||||
|
||||||||||
| Type | Sketch | parabola equation | Focus at Vertex |
Directrix Symmetry |
||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 |  |
x2 = 2py |
|
|
||||||
| 2 | 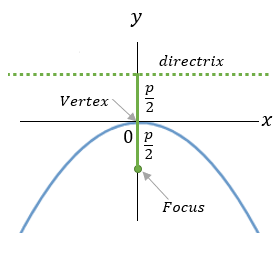 |
x2 = −2py |
|
|
||||||
| 3 | 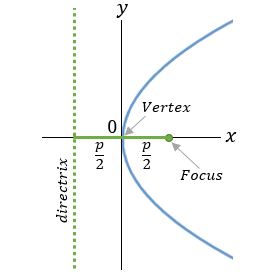 |
y2 = 2px |
|
|
||||||
| 4 | 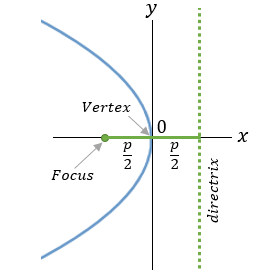 |
y2 = −2px |
|
|
||||||
|
||||||||||
| Type | sketch | parabola equation | Focus at Vertex |
Directrix Symmetry |
||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 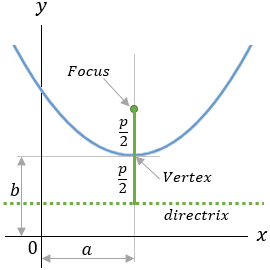 |
(x − a)2 = 2p(y − b) |
|
|
||||||
| 2 | 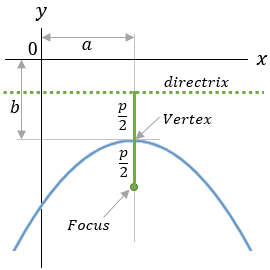 |
(x − a)2 = −2p(y − b) |
|
|
||||||
| 3 | 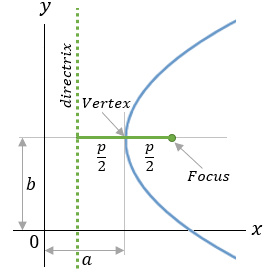 |
(y − b)2 = 2p(x − a) |
|
|
||||||
| 4 | 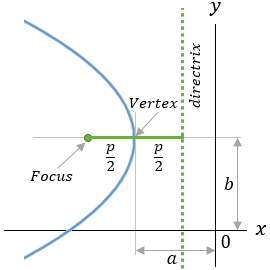 |
(y − b)2 = −2p(x − a) |
|
|
||||||
|
|||||||||||||
|
|||||||||||||
|
|||||||||||||
|
|||||||||||||
|
|||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
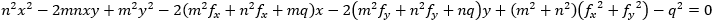
We can see that the signs of A and C must be positive (equals to square values).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||
|
Given the parabola x2 + 2y − 3x + 5 = 0, find the vertex, focus, directrix and the axis of symmetry.
|
||||||
|
By the method of completing the square we write the equation of the parabola as:
From the last equation we notice that a = 3/2 b = −11/8 and p = 1
|
||||||
|
||||||||||||||
|
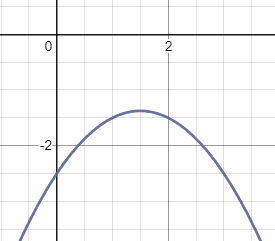
Given the parabola y2 −4y + 2x + 7 = 0, find the vertex, focus, directrix and axis of symmetry.
|
||||||||||||||
|
We will solve the general solution of the parabola equation: y2 + Ay + Bx + C = 0
By the method of completing the square we write the equation of the parabola as:
From the parabola given values we have: A = −4 B = 2 C = 7
From the last equation we see that the coordinate of the vertex is:
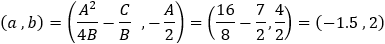
The sign of B is negative so the parabola open side is to the left direction.
|
||||||||||||||
|
||||
|
Find the coordinate of the foci and the directrix equation of the parabola given by the equation
y2 = −12x. |
||||
|
||||
|
||||||||||||||
|
Given the parabola x2 − 2x − 2y + 3 = 0, find the vertex, focus, directrix and axis of symmetry.
|
||||||||||||||
|
||||||||||||||
|
|||||||||||||
|
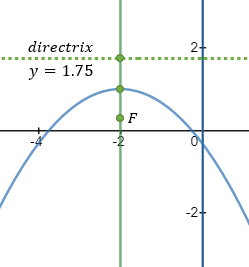
Given the directrix line of a parabola by the equation y = 1.75 and the focus at the point
F(−2 , 0.25). Find the equation of the parabola and the vertex and the symmetry line equations. |
|||||||||||||
|
|||||||||||||
|
||||||||||||||||||||||||||||
|
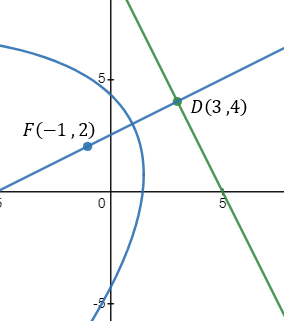
Given the focus of a parabola at (1 , 4) and the directrix equation x + y − 9 = 0 find the equation of the parabola and the coordinates of (xd , yd).
|
||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||
|
|||||||
|
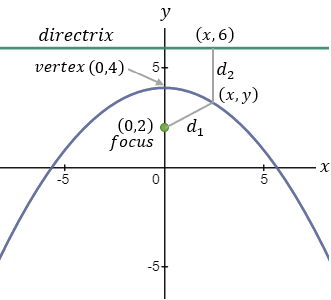
The focus of a parabola is located at the point (0 , 2) and the vertex at (0 , 4) find the
equation of the parabola. |
|||||||
|
|||||||
|
|||||||||||
|
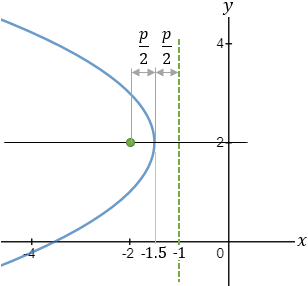
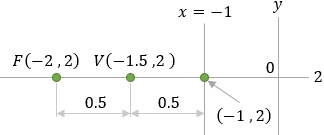
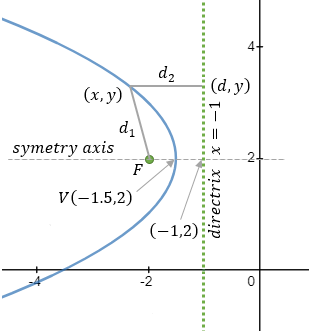
The vertex of a parabola is located at the point (−1.5 , 2) and the directrix equation is
x = −1 find the coordinate of the vertex and the equation of the parabola. |
|||||||||||
|
|||||||||||
|
||||||||||||||||||||
|
Find the transformation equations from the polynomial form x2 + ax + by + c = 0 to the standard form of the parabola (x + h)2 = p(y + k) and vice verse.
|
||||||||||||||||||||
Now we will change the parenthesis value into square expression
From the last expression we can see that
p is twice the distance from the focus to the directrix line p = |b| / 2
The open side of the parabola is pointing down if b is negative and pointing up if b is positive.
|
||||||||||||||||||||
|
|||||||
|
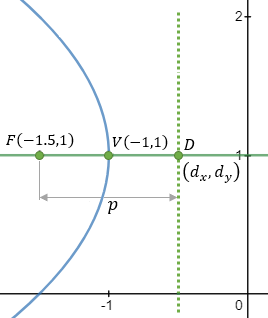
The focus of a parabola is located at the point (−1.5 , 1) and the vertex at (−1 , 1) find the
equation of the parabola the equation of the directrix and the equation of the symmetry line. |
|||||||
The directrix line is vertical and is passing through the point (−0.5 , 1) x = − 0.5
And the symmetry line equation from the sketch is: y = 1
|
|||||||
|
||||||||||||||||||
|
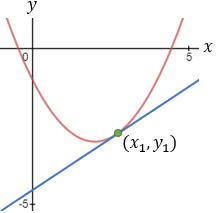
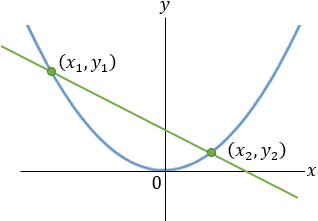
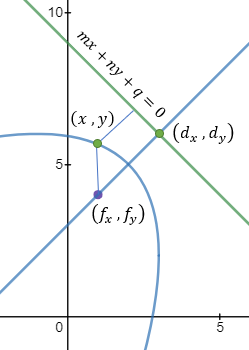
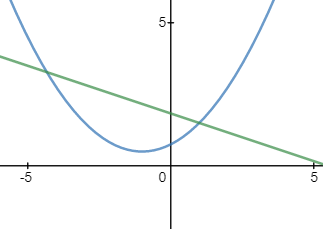
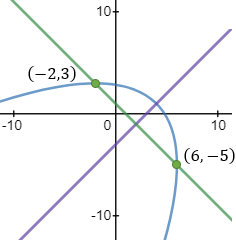
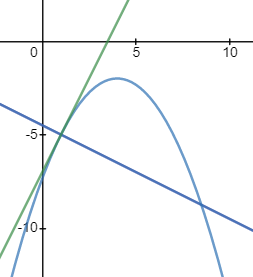
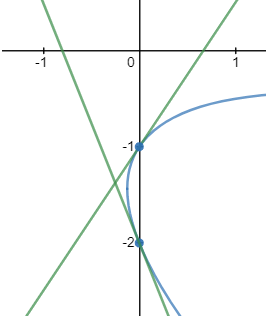
Find the general expression for the intersection of a parabola x2 + Ax + By + C = 0
and the line y = mx + q
With the expression developed find the intersection of the following parabola and line
x2 + 2x − 4y + 3 = 0 and the line x + 3y − 5.5 = 0. |
||||||||||||||||||
And the intersection points are (−4.33 , 3.28) and (1 , 1.5)
|
||||||||||||||||||
|
||||||
|
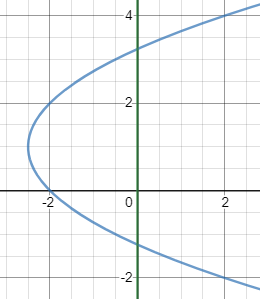
Find the intersection points of a parabola (y − 1)2 − 2(x + 2.5) = 0 and the lines a) x = 0 and b) the line y = 0.
|
||||||
And the intersection points are (0 , −1.24) and (0 , 3.24)
b) Substitute the line value y = 0 to the parabola equation we get: −2x − 4 = 0
It can be seen that there is only one solution for x and it is at x = −2 therefore only one intersection point exists at (−2 , 0)
|
||||||
|
||||||||||||||||||||||||||||||||||
|
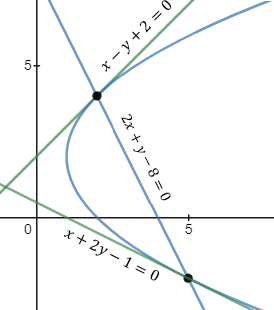
Find the intersection points of the a parabola x2 − 2xy + y2 + 10x + 22y − 71= 0 and the lines a) x + y − 1 = 0. b) x = 4. c) y = 0. Also derive a general expression for the intersection points.
|
||||||||||||||||||||||||||||||||||
|
a) Substitute the value of y from the line equation y = − x + 1 into the parabola equation.
x2 − 2x (− x + 1) + (− x + 1)2 + 10x + 22( − x + 1) − 71 = 0
b) Substitute x = 4 into the parabola equation: 16 − 8y + y2 + 40 + 22y −71 = 0
y2 + 14y − 15 = 0
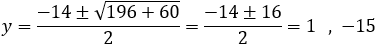
c) Substitute y = 0 into the parabola equation: x2 + 10x −71 = 0
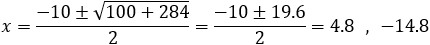
The general expression for the intersection points of:
Substitute the value of y into the equation of the parabola to get the values of x:
We got a quadratic equation and the solutions are the values of x. The values of y can be found according to equation (2) .
Substitute the value of x into the equation of the parabola to get the values of x:
We got a quadratic equation and the solutions are the values of y. The values of x can be found according to equation (2) .
|
||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||
|
Find the intersection points of the parabola (y − 2)2 = 4(x − 1) and the lines
2x + y − 8 = 0. Also find the tangent lines at the intersection points. |
||||||||||||||||||||||||||||
Line equation when a point and the slope are given is: y = mx + y1 − mx1
|
||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
|
Find the general equation of the line perpendicular to the parabola given by the equation
(x + h)2 = p(y + k) Then use the equation to find the perprndicular line to the parabola (x − 4)2 = −3(y + 2) at the point (1 , −5). |
||||||||||||||||||||||||||
If the tangency point is at (x1 , y1) then the equation of the perpendicular line is:
|
||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||
|
A parabola is given by y2 −2y −2x − 4 = 0, find, a) the equation of the tangent line at a point on the parabola where y = 4 and b) the tangent lines when x = −2.
|
||||||||||||||||||||||||||||||
|
By applying the implicit derivation on the parabola, we get the slope of the tangent line:
b) To find the y value of the point x = −2 we must solve the equation y2 − 2y −2x − 4 = 0
The solutions are y1 = 0 and y2 = 2 and the two tangent points are: (−2 , 0) and (−2 , 2)
|
||||||||||||||||||||||||||||||
|
|||||||||||||||||||
|
Find the equations of the tangent lines to the parabola given by the equation (y + 1)2 = x − 5
at the point where x = 6. |
|||||||||||||||||||
|
First we find the corresponding y values at x = 6: (y + 1)2 = 6 − 5
Solving this equation, we get: y2 + 2y = 0 and the solutions are y1 = 0 and y2 = −2
Now applying the implicit derivation on the parabola, to get the slope dy/dx of the tangent line:
Substitute the values of y into equation (1) in order to find the slopes of the tangent lines:
|
|||||||||||||||||||
|
|||||||||||||||||||||
|
Find the equations of the tangent lines to the tilted parabola given by the equation
x2 + 4xy + 4y2 − 2x + 12y + 8 = 0 and the intersection points of the line x = 0 and the parabola. |
|||||||||||||||||||||
|
First step is to find the coordinates of the line and parabola so we shell substitute the value of the line x = 0 into the parabola equation y2 + 3y + 2 = 0
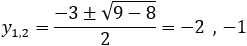 We found the two intersection points (0 , −1) and (0 , −2) and we have to find the tangent lines at those points.
To find the slope of the tangent line we shell explicitly derivate the equation of the parabola
|
|||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
|
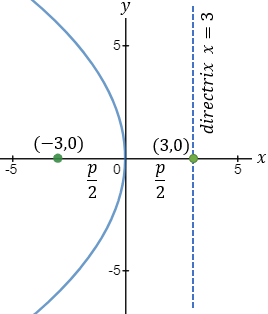
Find the equation and the vertex point of a parabola. If the focus point is at (−1 , −2) and directrix at the line x − 2y + 3 = 0.
|
||||||||||||||||||||||||||||||||||||
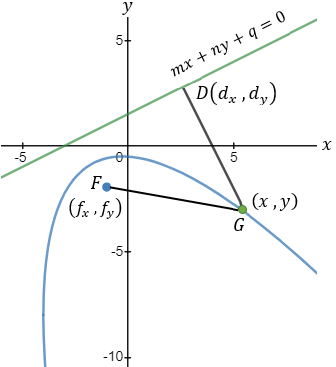
The vertex is located half way between the focus and the point G.
Point G is the intersection of the symmetry line and the directrix.
The symmetry line is passing through the focus and is perpendicular to the directrix line.
|
||||||||||||||||||||||||||||||||||||
|
|||||||||||||
|
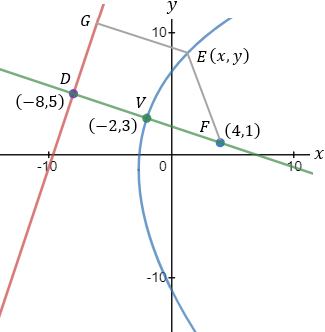
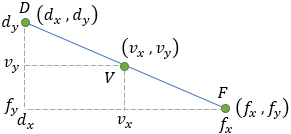
Find the equation of a parabola with focus at point (4 , 1) and vertex at point (−2 , 3) .
|
|||||||||||||
According to the parabola definition the distance EG = FE
|
|||||||||||||
|
|||||||||||||
|
Find the equation of a parabola with focus at point (−1 , 2) and the intersection point of the symmetry line and the directrix at (3 , 4) .
|
|||||||||||||
According to the parabola definition the distance EG = FE
|
|||||||||||||
|
|||||||||||||||||||||||||||||
|
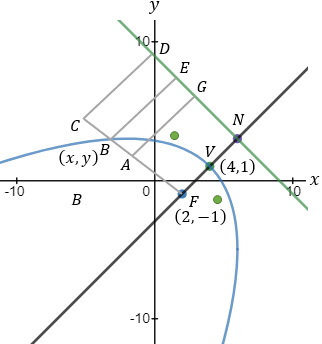
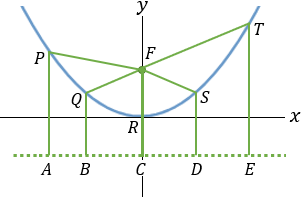
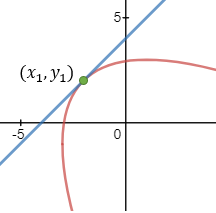
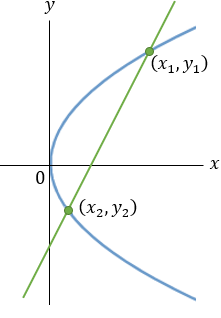
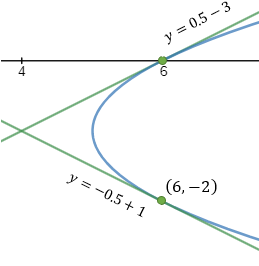
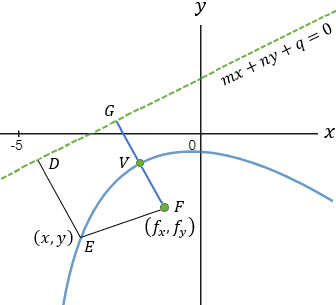
Given a parabola with focus at point (2 , − 1) and vertex at point (4 , 1) determined if points
(1 , 3) and point (5 , − 2) are inside or outside the parabola. |
|||||||||||||||||||||||||||||
And the coefficients are: A = 1 B = 1 C = −9
Now we have to find the relations between the lengths FB and BE
|
|||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
|
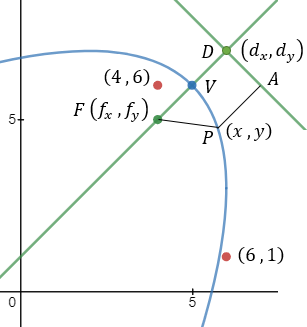
Given the parabola x2 − 2xy + y2 + 10x + 6y − 87 = 0 determined if the points (4 , 6) and the
point (6 , 1) are inside or outside of the parabola. |
||||||||||||||||||||||||||||||||||||
|
According to example 5b the value of q from eq (9) is:
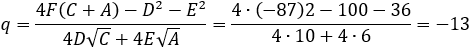
The directrix equation according to slope and point (dx , dy) is: y = mx + (y1 − mx1)
According to the parabola definition we have: FP = PA (where P is the point to verify).
|
||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||
|
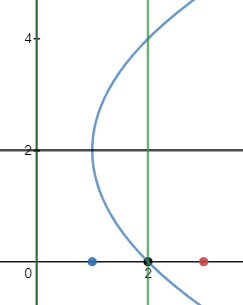
Given the parabola y2 − 4y − 4x + 8 = 0 determined if the points (1 , 0) and (2 , 0) and (3 , 0)
are inside or outside of the parabola. |
|||||||||||||||||||||||||||||||||||||||||||||
According to equations (14) and (15) the value of the intersection of symmetry axis and the directrix is (6 , 7)
The directrix equation is passing through point (0,2) so the equation of the directrix is x = 0
According to the parabola definition we have: FP = PA (where P is the point to verify).
|
|||||||||||||||||||||||||||||||||||||||||||||


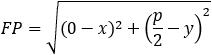
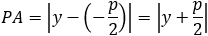
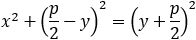
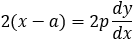
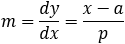
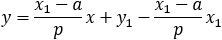
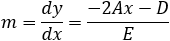
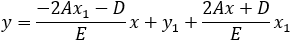
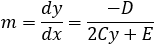
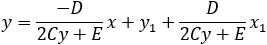
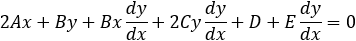
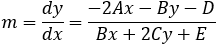
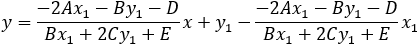
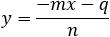
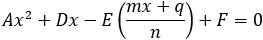
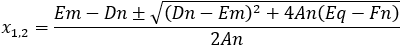
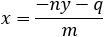
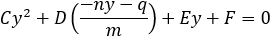
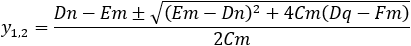
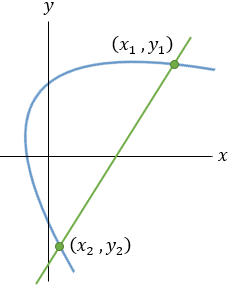
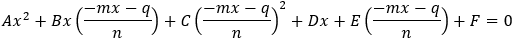
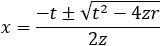
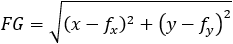
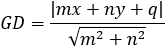
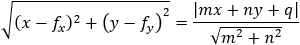
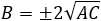
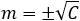
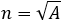
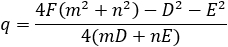

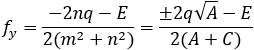
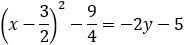
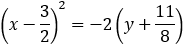
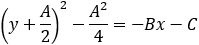
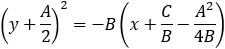
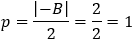
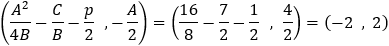
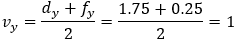
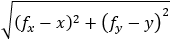
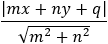
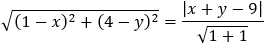
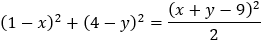
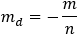
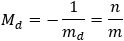
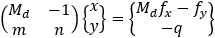
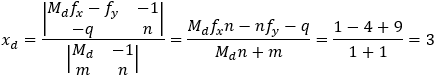
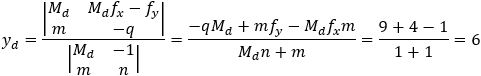
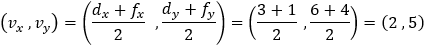
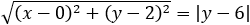
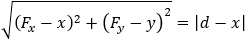
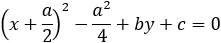
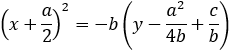
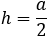
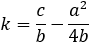
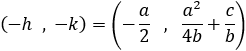
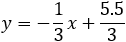
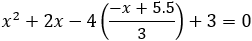
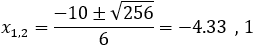
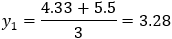
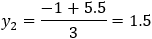
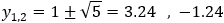
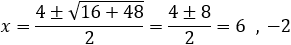
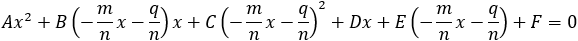
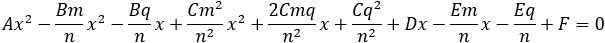
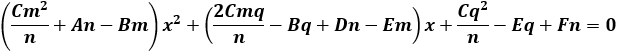
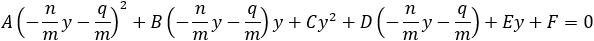
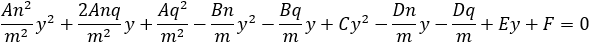
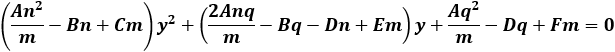
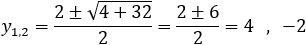
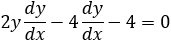
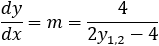
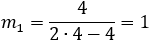
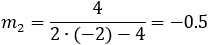
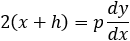
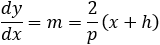
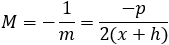
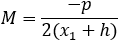
![p/2(x_1+h) x+y-[y_1+(px_1)/2(x_1+h) ]=0](/TrigoCalc/Circles2/Parabola/Eq/Ex3d5.png)
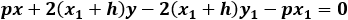
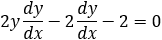
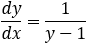
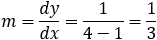
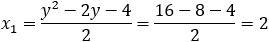
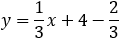
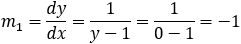
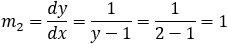
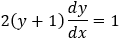
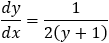
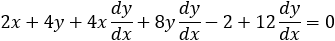
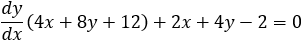
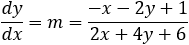
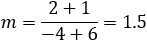
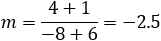
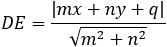
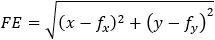
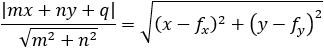
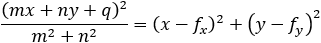
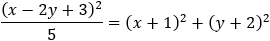
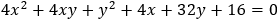
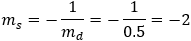
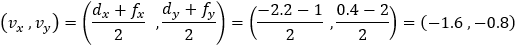
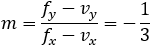
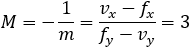
![[v_x-(f_x-v_x ) ,v_y+(v_y-f_y )]](/TrigoCalc/Circles2/Parabola/Eq/Ex5b0.png)