Circle basic laws

| Area of a circle (A) | 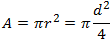 |
| Circumference of a circle (P) | 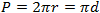 |
| π value up to 21 decimal places | π = 3.141 592 653 589 793 238 462 ... |
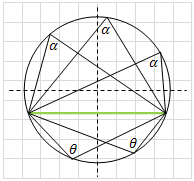 |
Inscribed angles (1) All inscribed angles intercepted by the same arc or cord and lies on the same side of the cord are equal.
(2) Sum of opposite angles drawn from the same cord are equal to 180°, α + θ = 180°
(3) If the cord coincides with the diameter of the circle, then the inscribed angle is a right angle α = θ = 90°.
|
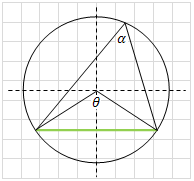 |
Central and inscribed angles If central angle θ and inscribed angle α intercepts the same cord or arc then:  |
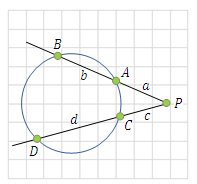 |
Intersecting secants theorem If a line from a point P intersects the circle at two different locations, then: 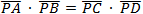 We can also write:(a + b) a = (c + d) c If line PD = c is tangent thenc2 = (a + b) a |
 |
Tangent and secant line theorem The value of an angle formed by a secant or tangent line drawn from a point P outside the circle equals the half of the difference of the intercepted arcs or central angles. 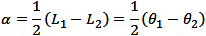 θ1 θ2 are the central angles of the shown arcs.
|
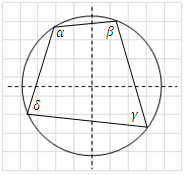 |
Cyclic quadrilateral The sum of the opposite angles in an inscribed (cyclic) quadrilateral are equal to 180°. α + γ = 180°
β + δ = 180°
|
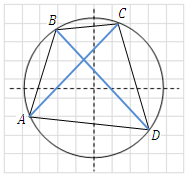 |
Ptolemy's theorem The product of the diagonals of a cyclic quadrilateral equals the sum of the products of the opposite sides. 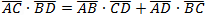 |
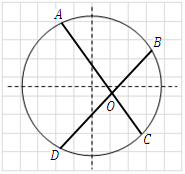 |
Intersecting chord theorem The product of the two segments created by intersecting of two chords are equal. 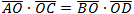 |
