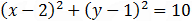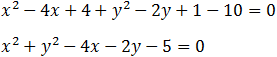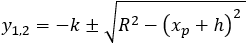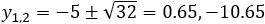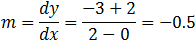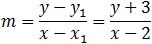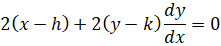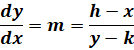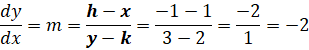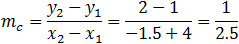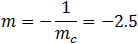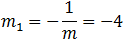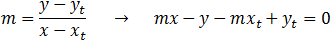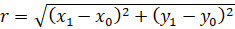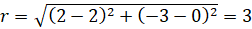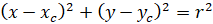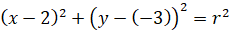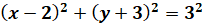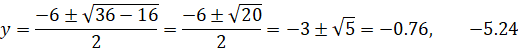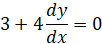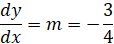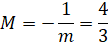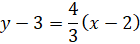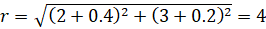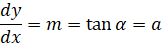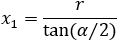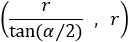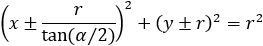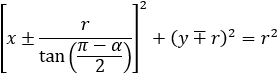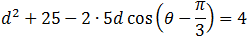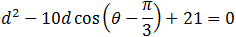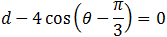Circle equation

circle equations summary

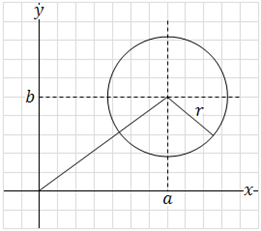

This circle’s center is located at coordinate (a , b) and has a radius of r. This equation can be manipulated to get an additional form of a circle:
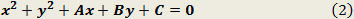
The circle equation can be presented by the following forms:
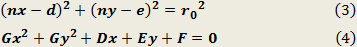
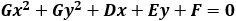
Relations between the coefficients of equations (1), (2), (3) and (4) are:
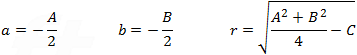
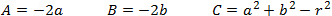
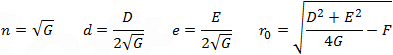
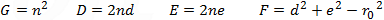
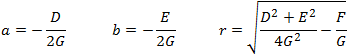
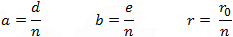
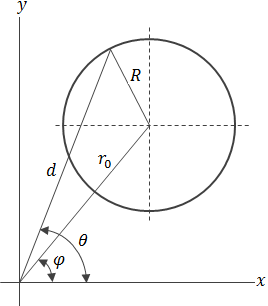
Circle polar coordinates
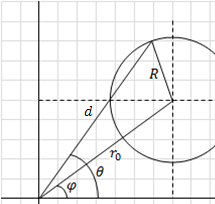
In polar coordinates the center of the circle is described by: (r0 , φ) that is the distance from the origin to the center and the angle to the center.
General form of a circle equation in polar form is obtained by using the law of cosines on the triangle that extends from the origin to the center of the circle (radius r0) and to a point on the circle (radius r) and back to the origin (side d).
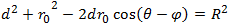
If the center of the circle lies on the x axis, then the circle equation becomes:
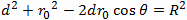
If the center of the circle lies on the y axis, then the circle equation is:
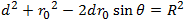
In case the center of the circle coincides with the origin then
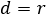
|
||||
|
Find the equation of a circle with a center at (2 , 1) and passing through the point (3 , 4).
|
||||
|
Because the given point lay on the circle then the distance between the circle center and the point is the radius. The distance is given by:
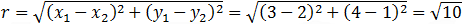
|
||||
|
||||||||
|
Find the points on the circle (x − 2)2 + (y + 5)2 = 36 whose x is equal to 4.
|
||||||||
|
First we will solve the general case of the circle: (x + h)2 + (y + k)2 = R2 if we
set the x point as xp then we have.
(xp + h)2 + (y + k)2 = R2
|
||||||||
|
|||||||||||
|
Find the equation of the line normal to the circle x2 + y2 + 4y −1 = 0 and passing through the point
(2 , −3). |
|||||||||||
First, we have to find the equation of the line stretching from the center of the circle to the given point. The center of the circle can be found by the procedure for completing the square (a + b)2 = a2 + 2ab + b2.
This is a circle with a radius of square root of 5 and center at (0 , −2 ).
|
|||||||||||
|
||||||||||||||||||||
|
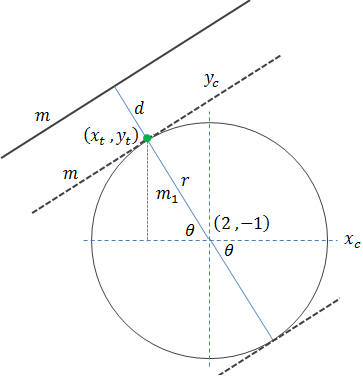
Find the equation of the tangent line to the circle x2 + y2 + 3x −4y −1 = 0 and a point (−4 , 1) which lies on the circle.
|
||||||||||||||||||||
The solution of this problem can be solved in different ways we will show two methods. First by implicit differentiation of the circle equation, this will give us the slope of any point on the circle and then find the equation of the line by the slope and the given point.
The second method is to find the slope of the line connecting the center of the circle to the given point and then the tangent line slope is perpendicular to this slope, hence equal to minus the reciprocal of the slope.
We get the same slope as in the first method.
|
||||||||||||||||||||
|
||||||||||
|
Find the equation of the tangent line to the circle (x + 1)2 + (y − 2)2 = 5 and a point (1 , 3) which lies on the circle.
|
||||||||||
|
If we denote the center of the circle by the point (h = −1 , k = 2) then the circle eaution is: (x − h)2 + (y − k)2 = R2
By implicit differentiation of the circle equation, we will find the slope of any tangent line to the circle.
According to the tangent line equation we have x1 = 1 and y1 = 3.
|
||||||||||
|
||||||||||||||||
|
A circle is given by the equation (x − 2)2 + (y + 1)2 = 9. A line x − 4y + 15 = 0 is drawn outside the circle. Find the tangency point if the line is brought closer to the circle by kipping the same incline until it touches the circle.
|
||||||||||||||||
|
||||||||||||||||
|
|||||||
|
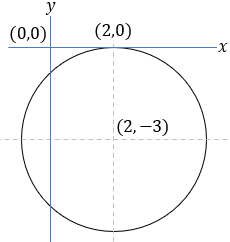
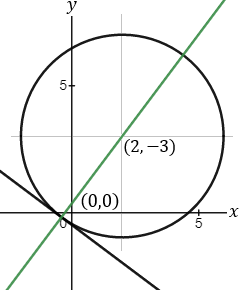
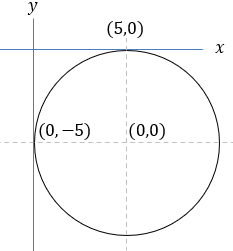
A circle's center is located at the point (2, -3). Find the equation of the circle that is tangent to the x axis, and also find the intersection points of the intersection of the circle with the y axis.
|
|||||||
In order to find the intersection points with the y axis substitute x = 0 in the circle's equation. We get the quadratic equation: y2 + 6y + 4 = 0
And the intersection points are: (0 , −0.76) and (0 , −5.24) |
|||||||
|
||||||||||
|
Find the equation of a circle with center at (2 , 3) that is tangent to the line 3x + 4y + 2 = 0.
|
||||||||||
|
||||||||||
|
||||
|
Find the equation of a circle which is tangent to both axii x and y at the 4th quadrant (x > 0 , y < 0) and has a radius of 6.
|
||||
|
||||
|
||||||||||||
|
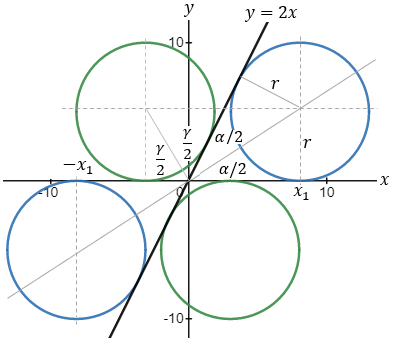
Find all the equations of the circles which are tangent to the x axis and the line y = 2x and have a radius of 6.
|
||||||||||||
The equations of the upper right and lower left circles (blue circles) are:
The equations of the lower left and upper right circles (green circles) are:
Notice that each circle center is located at a different quadrant. |
||||||||||||
|
||||||||||||||||||||||
|
Circle center is given by the polar coordinate to be (5 , pi/3). Find the equation of the circle if the radius is 2. Investigate the cases when
circle center is on the x axis and if the center is on the y axis, and in the origin.
|
||||||||||||||||||||||
|
||||||||||||||||||||||