☖ Home ⇄ Units Converter ⧉ Geometry Σ Math ✈ Physics 〶 Electricity

Three tangent circles calculator

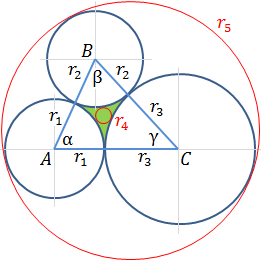
Print 3 tangent circles summary
3 tangent circles
A(r1) 
L(r1) 
A(r2) 
L(r2) 
A(r3) 
L(r3) 
r1
r2
r3
Green area
Green area circumference
Triangle ABC area
Angle α
Angle β
Angle γ
Inner circle radius   r4
Outer circle radius   r5
Area between three tangent circles
Example 1
Example 2

Area between three tangent circles summary

Print area between three tangent circles
Triangle ABC area
We define the length of the triangle ABC sides as:
a = r2 + r3
b = r1 + r3
c = r1 + r2

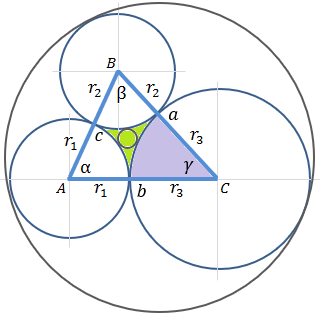
The area of triangle ABC by Heron's formula is:

Triangle ABC area

After substituting the values of a, b and c we get:

A_T=√((r_1+r_2+r_3 ) r_1 r_2 r_3 )

The sectors areas are:

Sectors area

And the area between the 3 tangent circles (green area) is:
A=A_T-A_A-A_B-A_C

The angles of the triangle ABC can be found by cosine law:

Triangle angles

The green area circumference is the sum of the arcs lengths formed by the angles   α r1,   β r2   and   γ r3:

P=αr_1+βr_2+γr_3

The radii of the four tangent circles are related to each other according to the Descartes circle theorem:

Descartes' theorem

If we define the curvature of the  nth  circle as:
Circle curvature

Notice that when  k = 0  then the radius is infinity, that means that the radius is a straight line.

The plus sign means externally tangent circle like circles   r1 , r2 , r3 and r4   and the minus sign is for internally tangent circle like circle   r5 in the drawing in the top.

Then the Descartes circle theorem is:
( k1 + k2 + k3 + k4 ) 2 = 2 ( k12 + k22 + k32 + k42 )

And the curvature of the circles k4 and k5 which are called the Soddy circles are:

Inner circle radius

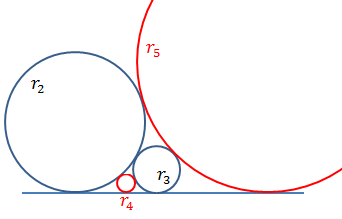
Descartes' circle theorem

If circle  r1  is a straight line then   r1 = ∞
and the curvature is    k1 = 1 / r1 = 0
The curvature of the two red Soddy circles is simply:

Inner circle radius

Example 1 − Area between three tangent circles

Print area between three tangent circles example
Two circles of radii 9cm and 4cm are tangent to each other and are placed on a straight surface. Find the area and the circumference contained by the circles at the tangent points.
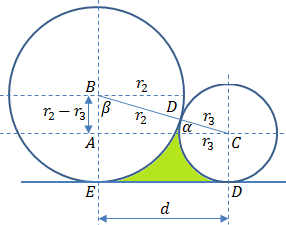
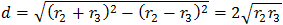
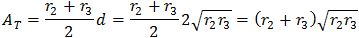
Descartes' circle theorem
First, we will find the value of   d
Descartes' circle theorem Descartes' circle theorem
The area of the trapezoid   BCDE   is:
Descartes' circle theorem
Area of the green surface is:
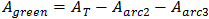
Green surface area

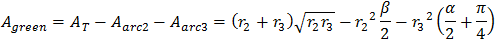
Green area

Note: In the calculations we assume that R2 is bigger then R3, therefore, to find the angle of sector r3 we must add to angle  β,   90 degrees  (pi/2).

The area of the trapezoid is:
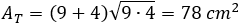
A_T=(9+4) √(9∙4)=78
Angles α and β are:
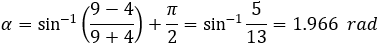
α=sin^(-1)⁡〖(9-4)/(9+4)〗=sin^(-1)⁡〖5/13〗=0.395 rad

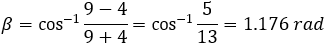
β=cos^(-1)⁡〖(9-4)/(9+4)〗=cos^(-1)⁡〖5/13〗=1.176 rad

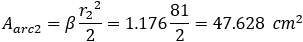
A_arc2=β 〖r_2〗^2/2=1.176 81/2=47.628 〖cm〗^2

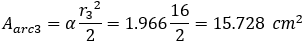
A_arc3=α 〖r_3〗^2/2=1.966 16/2=15.728 〖cm〗^2

The circumference of the green area is:
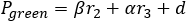
P_green=βr_2+αr_3+d

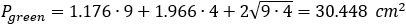
P_green=1.176∙9+1.966∙4+2√(9∙4)=30.448 〖cm〗^2

Example 2 − Area between three tangent circles

Print area between three tangent circles example
Given three circles with radii of 2, 3 and 4. find the area contained by these circles and the circumference contained by the circles at the tangent points.
Descartes' circle theorem
Set the radii as:     r1 = 2   r2 = 3   r3 = 4  

The ribs of the triangle ABC will be:

a = r2 + r3 = 3 + 4 = 7

b = r1 + r3 = 2 + 4 = 6

c = r1 + r2 = 2 + 3 = 5

Now we can find any angle of the triangle by cosine law:

a^2=b^2+c^2-2bc cos⁡α

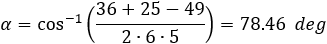
α=cos^(-1)⁡((36+25-49)/(2∙6∙5))=78.46 deg

The area of triangle ABC is:
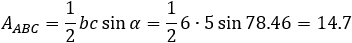
A_ABC=1/2 bc sin⁡α=1/2 6∙5 sin⁡78.46=14.7
Now find angle β the same way or by sines law:
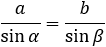
a/sin⁡α =b/sin⁡β

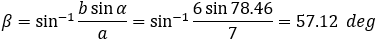
β=sin^(-1)⁡〖(b sin⁡α)/a〗=sin^(-1)⁡〖(6 sin⁡78.46)/7〗=57.12 deg

γ = 180 − α − β = 180 − 78.46 − 57.12 = 44.42 deg

Now the green area Ag can be calculated:

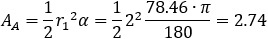
A_A=1/2 〖r_1〗^2 α=1/2 2^2 (78.46∙π)/180=2.74

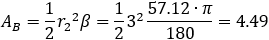
A_B=1/2 〖r_2〗^2 β=1/2 3^2 (57.12∙π)/180=4.49

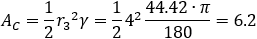
A_C=1/2 〖r_3〗^2 γ=1/2 4^2 (44.42∙π)/180=6.2

Ag = AABC − A1 − A2 − A3 = 14.7 − 2.74 − 4.49 − 6.2 = 1.27

The green area circumference Lg is the sum of the three arcs formed by the angles α, β and γ.

L1 = r1 α = 2 ‧ 78.46 ‧ pi / 180 = 2.74

L2 = r2 α = 3 ‧ 57.12 ‧ pi / 180 = 3

L3 = r3 α = 4 ‧ 44.42 ‧ pi / 180 = 3.1

Lg = L1 + L2 + L3 = 2.74 + 3 + 3.1 = 8.84