☖ Home ⇄ Units Converter ⧉ Geometry Σ Math ✈ Physics 〶 Electricity

Coplaner points calculator

Print coplaner points calculator
Input plane equation
x
 + 
y
 + 
z
 + 
= 0
Input 3 points to define a plane
Point 1
X1 
Y1 
Z1 
Point 2
X2 
Y2 
Z2 
Point 3
X3 
Y3 
Z3 
Test point
Xt 
Yt 
Zt 
Coplanar test:
Distance from plane:
Plane equation:
Coplanar point summary
example 1
example 2

Coplanar points summary

Print coplaner points summary
Coplanar points
Coplanar points
Points that are located on a plane are coplanar.
3 points always creates a plane, so they are always coplanar.

4 points are coplanar if the volume created by the points is 0.

|■(x_0&y_0&■(z_0&1)@x_1&y_1&■(z_1&1)@■(x_2@x_3 )&■(y_2@y_3 )&■(■(z_2&1)@■(z_3&1)))|
In vector format the points are coplanar if the vectors connecting one point to the other three points satisfy
the scalar triple product:
v_1∙(v_2×v_3 )=0
The vectors are:
v1 = (x1 − x0)i + (y1 − y0)j + (z1 − z0)k
v2 = (x2 − x0)i + (y2 − y0)j + (z2 − z0)k
v3 = (x3 − x0)i + (y3 − y0)j + (z3 − z0)k
If any three points determine a plane, then additional points can be checked for coplanarity by measuring the distance of the points from the plane, if the distance is 0 then the point is coplanar.
If the Plane equation is:
Ax + By + Cz + D = 0
Then distance of a point (xn , yn , zn) from the plane is:
Distance of a point to plane

To check if the given points are colinear (all points located on the same line) use the equation:

(x2 − x1)(y3 − y1) − (x3 − x1)(y2 − y1) = 0

Coplanar points - Example 1

Print coplanar points example
Example: Find if the following points are coplanar: (3, -3, 2), (1, 0, 1), (1, 1, 0), (0, 1, 1).
Solution: the three vectors are:
v1 = − 2i + 3j − k
v2 = − 2i + 4j − 2k
v3 = − 3j + 4j − k
In order to find if all 4 points are coplanar we can check the triple product:     v1 ∙ (v2 × v3) = 0
v_2×v_3=|■(i&j&k@-2&4&-2@-3&4&-1)|=i+j+k
And the triple product is equal to: v1 ∙(v2 × v3) = (-2i + 3j - k)∙(i + j + k) = − 2 + 3 - 1 = 0
The resulting 0 indicates that the points are coplanar.
Another way to check if the points are coplanar is by calculating the volume produced by the 4 points, this process is tedious because we have to calculate the determinant of a 4th degree matrix:
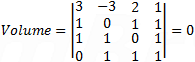Volume between 4 points the volume is zero therefore these 4 points are coplanar.
Now any additional points can be checked by calculating the distance of the points from the plane, which is defined by the previous points, for example if we have another point let say the point (-2, 3, 1).
The coefficients of the equation of the plane are:       A = 1       B = 1       C = 1       D = − 2
x + y + z − 2 = 0
And the distance from this plane to the point (-2, 3, 1) is:
d=|Ax_n+By_n+Cz_n+D|/√(A^2+B^2+C^2 )=|1∙(-2)+1∙(3)+1∙(1)-2|/√(1+1+1)=0
Because the distance is zero this additional point is also coplanar related to the other points.

Triple product - Example 2

Print coplanar points example
Example:
A plane is given by two vectors   v2 = i + 2k   and   v3 = 2i − 3j + k find if the point   (4, 1, −1), is coplanar.
Solution:
We set the vector v1 starting from the origin as v1 = 4i + j − 1
v_2×v_3=|■(i&j&k@-2&4&-2@-3&4&-1)|=i+j+k

Now we will use the triple product method to determine if the given point denoted by v1 is coplanar. If the point is coplanar then the vector v1 will also located on the plane formed by v2 and v3.

The triple product states that   n = v1 • (v3 ╳ v2)

v_n=(v_2×v_3 )=|■(i&j&k@2&-3&1@3&2&0)|=-2i+3j+11k

Vector vn is perpendicular to our plane as a result of the cross product definition.

From the dot product with v1 we find that:
cos⁡θ=(A∙B)/|A||B| =(A_x B_x+A_y B_y+A_z B_z)/(√(A_x+A_y+A_z ) √(B_x+B_y+B_z ))

The result of the dot product is the cos of the angle between the two vectors  v1  and  (v2 ╳ v3). If the result is   cos θ = 0 then θ  is 90 degree and in the direction of  vn, and hence located also on the plane, and the point is coplanar.

cos⁡θ=(2∙3-3∙2+1∙0)/(√(4+9+1) √(9+4+0))=0

The angle   θ = cos-1(0) = 90 degree   and the point is coplanar.