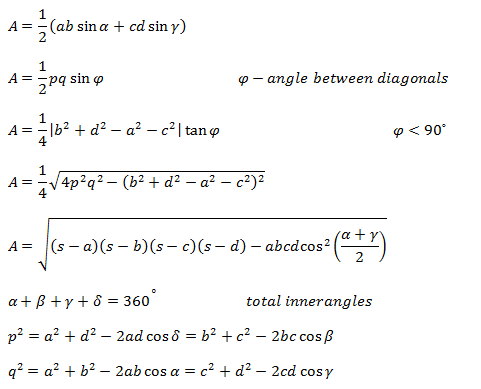|
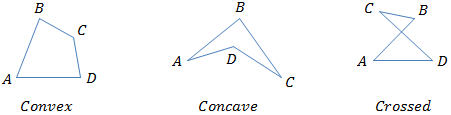
Four sides of an irregular quadrilateral can be arranged in convex, concave or crossed shape.
(We assume that the vertices are connected by the sequence from A to B then to C and to D and finally back to A)
Because any arbitrary 4 sides can form a convex, concave or crossed quadrilateral it is mandatory to define the exact form.
In order to draw a quadrilateral closed shape the following inequalities must be fulfilled:
| a + b + c > d |
| b + c + d > a |
| c + d + a > b |
| d + a + b > c |
Any quadrilateral shape can be divided into 2 triangles.
The area of a convex quadrilateral can be expressed in one of the following formulas:
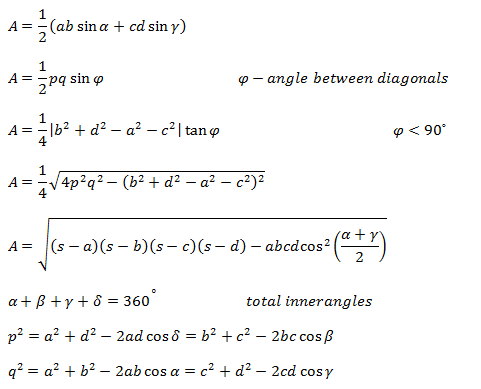
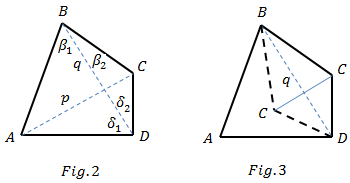 |
It can be seen from Fig. 3 that folding triangle BCD along q axis forms a concave quadrilateral.
The question now is how can we estimate if folding the triangle will form a concave or crossed shape.
From fig. 2 we can see that if
β1> β2 and δ1> δ2
are both true then the new shape will be concave else if one of the criteria is false the new shape is a crossed
quadrilateral. If both criteria are false then it is a concave shape but triangle ABD is folded into triangle BCD instead.
|
|