☖ Home ⇄ Units Converter ⧉ Geometry Σ Math ✈ Physics 〶 Electricity

Sphere defined by 4 points calculator

Print sphere defined by 4 points
Input points by certasian coordinates
Point 1 X1  Y1  Z1 
Point 2 X2  Y2  Z2 
Point 3 X3  Y3  Z3 
Point 4 X4  Y4  Z4 
Input points by spherical coordinates
Point 1 r1  1  1 
Point 2 r2  2  2 
Point 3 r3  3  3 
Point 4 r4  4  4 
Center point coordinates:           X:       Y:       Z:  
Radius of sphere:           r:   
Sphere volume:
Sphere surface area:
Sphere equation:         x2 + y2 + z2 + x + y + z + = 0
                                 

Sphere defined by 4 points summary

Print sphere defined by 4 points summary
Sphere equation.
The equation of a sphere with center at point (h, k, l) is:
(x − h)2 + (y − k)2 + (z − l)2 = r2
The equivalent form of sphere equation is:
x2 + y2 + z2 + Dx + Ey + Fz + G = 0
The relations between the coefficients are:
D = − 2h           E = − 2k           F = − 2l           G = h2 + k2 + l2 − r2
The angle θ between two points
P1 (x1 , y1 , z1) and P2 (x2 , y2 , z2) both points lays on the sphere.
Angle of two points and sphere center
The arc length between those two points is:     L = θr
The equation of sphere passing through 4 points: P1 (x1 , y1 , z1)
P2 (x2 , y2 , z2) , P3 (x3 , y3 , z3) and P4 (x4 , y4 , z4).

Because each point is located on the sphere, we get 4 equations with the unknowns coefficients D, E, F and G they can be valuated by solving the system of the equations by matrix methods (Cramer's rule).

D coefficient E coefficient
F coefficient G coefficient
Where: t1 = −(x12 + y12 + z12) t2 = −(x22 + y22+ z22)
t3 =−(x32 + y32 + z32) t4 =−(x42 + y42 + z42)
T is the determinant value T = T value
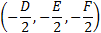The center of the sphere is at coordinate: Sphere center coordinate
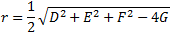The radius of the sphere is: Sphere center coordinate