Matrices Algebra Equations

Eigenvalues and eigenvectors

The system (λI − A) = 0 has a non trivial solution if and only if det |λI − A| = 0. If P denote the matrix of the eigenvectors and B denote the diagonal matrix with diagonal elements being the eigenvalues λ_i of A.

We can write:	AP = PB
	P^{− 1} AP = B or A = PBP^{− 1}

In this case, A is said to be similar to B.

Example: Find the eigenvalues and the eigenvectors of the matrix A =

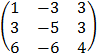From the eigenvalues equation we get the characteristic polynomial:

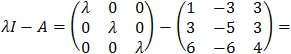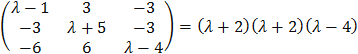The eigenvalues are the roots of the characteristic polynomial, and are: − 2, − 2, 4 this values are the diagonal values and has the same determinant value as matrix A. In order to find the eigenvectors, substitute first solution λ =− 2 into the characteristic matrix, the result is:

Those MathCalc reduce to one independent equation:	x − y + z = 0
Choose arbitrary y = 0 to receive the first eigenvector	x = 1, y = 0, z = − 1
Choose arbitrary z = 0 to get the second vector:	x = 1, y = 1, z = 0

Perform the same process with the third solution λ = 4 to get:

The result is two independent equations:	x + y − z = 0 and 2y − z = 0
Choose arbitrary y = 1 to receive the vector	x = 1, y = 1, z = 2

The three eigenvectors are:

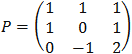We can see that the result is matching to the definition of the eigenvectors and eigenvalues:

Rotation Matrices

Rotation of a vector is performed by applying the rotation matrix R on the vector V. V^' = R × V

If the rows and columns of a rotation matrix R are orthogonal to each other and of unit length then the following relations are true:

R^T = R^{− 1} R^T R = RR^T = I detR = 1

Two-dimensional rotation

Rotation by θ counterclockwise

+θ counterclockwise
−θ clockwise

Rotation by θ clockwise

sin(−θ) = −sinθ
cos(−θ) = cosθ

Rotation by 90° counterclockwise

Rotation by 180° counterclockwise

Rotation by 270° counterclockwise

Three dimensional rotation (θ − x axis, ϕ − y axis, φ − z axis)

Rotation about
x axis

Rotation about>
y axis

Rotation about
z axis

Combined rotation in the direction of all axes can be done by multiplying the three rotation matrices in the x,y and z direction

Counterclockwise:	R_xyz = R_x(θ)∙R_y(ϕ)∙R_z(φ)
Mixed direction:	R_xyz = R_x(−θ)∙R_y(−ϕ)∙R_z(φ)

Rotation in the direction of two axes can be done by:

R_xy = R_x R_y

R_xz = R_x R_z

R_yz = R_y R_z

clockwise rotation matrix of the axes (vector is moved counterclockwise)
Note: the order of the rotation is important as rotation R_x (θ) R_y (ϕ) R_z (φ) is not equal to rotation
R_z (φ) R_y (ϕ) R_x (θ).

Counterclockwise rotation matrix of the axes (vector is moved clockwise)

Example:
Rotate the vector V = 2i + j

by 30° counterclockwise.

(Rotated vector) V ^' = R × V (R - Rotation matrix)

V^' = [2 cos(30°) − sin(30°)]i + [2 sin(30°) + cos(30°)]j
V^' = 1.23i + 1.87j

Example:
Rotate the vector V = i + j + k by an angle of 30° counterclockwise about the x axis, 45° clockwise about the y axis and 60° clockwise about z axis.

Step 1: rotation θ = 30° about x axis counterclockwise:

Step 2: rotation ϕ = 45° about y axis clockwise:

Step 3: rotation φ = 60° about z axis clockwise: