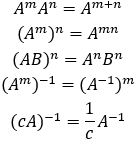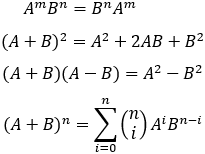Matrices overview

The notation of a matrix of size (m ✕ n) is defined as A(m ✕ n) = A(rows, columns)
A convenient shorthand which offers considerable advantage when working with system of
linear equations is by using the matrix notation.
Consider the set of linear equations of the form:
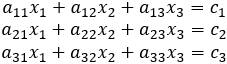
In matrix notation these equations may be represented as:
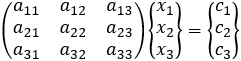
or AX = C
The terms of the matrix can be represented as:
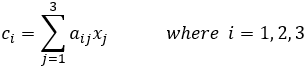
| Distributive law |
Left side A(B + C) = AB + AC
Right side (A + B)C = AC + BC
|
A(m ✕ n) B and C (n ✕ p)
A and B (m ✕ n) C(n ✕ p)
|
||
| Associative law |
Addition (A + B) + C = A + (B + C)
Multiplication (AB)C = A(BC)
|
(m ✕ n)
(n ✕ n)
|
||
| Scalar multiplication | (kA)B = A(kB) = k(AB) |
A(m ✕ n) B(n ✕ p) k any number |
||
| Commutative law |
Addition A + B = B + A
Multiplication not commutative
|
A and B (m ✕ n)
Because A∙B ≠ B∙A
|
||
| Other algebraic laws (k, v are constants) |
0 + A = A
k(A + B)= kA + kB
1 · A = A
(k + v)A = kA + vA
0 · A = 0
k(vA) = (kv)A
A + (−A) = 0
kA = 0 → k = 0 or A = 0
(−1)A = A
|
|||
| Matrices powers (c is constant) |
|
|||
Matrices Types

Matrices addition and multiplication

Matrices addition: A and B are of the same size m × n
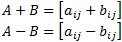
Scalar multiplication:
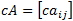
Matrices multiplication A (m × n) ∙ B (n × p) = C (m × p)
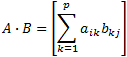
Example:
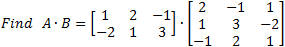
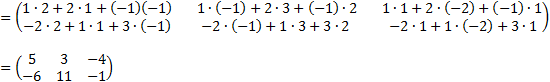
Determinants

Determinants - symbol: det A or |A|
The result of the determinant of a matrix (n ⨯ n) is a real number.
Size 2 matrix
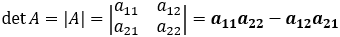
Size 3 matrix
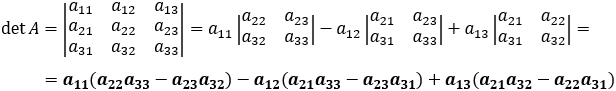
General form to evaluate determinant values:
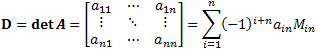
In this formula Min is the determinant of the submatrix of A obtained by deleting its ith row and nth column.
The determinant Min is called the minor of the element ain and his size
is (n-1) ⨯ (n-1).
Cofactors of matrix Aij
It is convenient to consolidate the quantity (-1)i+j and the minor Mij .
We define the cofactor Aij of the element aij in
determinant A as: Aij = (-1)i+jMij
Determinant’s properties:
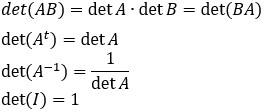
Example: Find the value of the determinant:
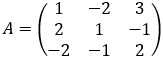
det A = 1 (1 * 2 − (- 1)(- 1))-(-2)(2 * 2 - (-1)(-2)) + 3 (2 * (-1) - 1 * (-2))
det A = 1 (2 − 1) + 2 (4 − 2) + 3 (− 2 + 2) = 5
Transposed matrix AT

Transposed matrix AT
Interchange of terms across the main diagonal
Interchange of terms across the main diagonal
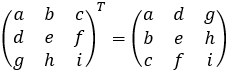
Transposed matrices properties:
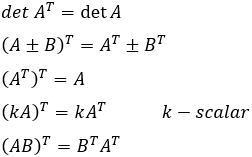
Example:
Find the transposed of the matrix.
Find the transposed of the matrix.
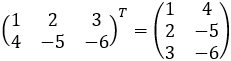
Note: The transposed size of an m ⨯ n matrix is n ⨯ m.
Inverse matrix A-1

Inverse matrix A-1 = B
The matrix A is inversible if there is a matrix B so that:
AB = BA = I then the matrix B is the inversed matrix of A.
Matrix I is the unit matrix. Thus the solution of A X = B can be written in the form X = A-1 B (where A is an n x n matrix and X and B are n x 1 matrices).
AB = BA = I then the matrix B is the inversed matrix of A.
Matrix I is the unit matrix. Thus the solution of A X = B can be written in the form X = A-1 B (where A is an n x n matrix and X and B are n x 1 matrices).
Inversed matrices properties:
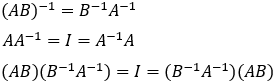
Example: Find the inverse of matrix A
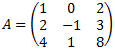
1. Add the unit matrix at the right:

2. Multiply first row by -2 and add it to the second row then multiply first row by -4 and add it to the third row to obtain:
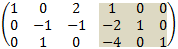
3. Add second and third rows to obtain:
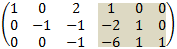
4. Subtract third row from second row:

5. Finally multiply third row by 2 and add it to the first row and multiply third row by -1 to get the unit matrix:
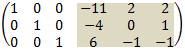
And the inverse of A is:
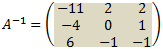
Rank of a matrix A

Rank of matrix A
A square matrix is said to be non-singular, if its determinant is not zero. The rank of an m ⨯ n matrix is
the largest integer r for which a non-singular r ⨯ r submatrix exists.
If A and B are an n ⨯ n matrices then: rank(A + B) ≤ rank A + rank B
Example: Find the rank of matrix A (4X3).
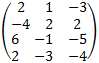
1. Multiply first row by 2 and add it to the second row.
2. Multiply first row by -3 and add it to the third row.
3. Subtract fourth row from the first row to get:
2. Multiply first row by -3 and add it to the third row.
3. Subtract fourth row from the first row to get:
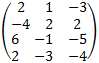
4. Add second row to the third row.
5. Subtract fourth row from second row to obtain:
5. Subtract fourth row from second row to obtain:
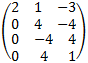
6. Add 2nd row to the 3rd row.
7. Add 3rd row to the 4th row to get:
7. Add 3rd row to the 4th row to get:
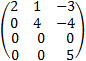
8. Remove the all 0 row to get the final 3 X 3 matrix.
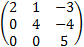
And the rank of matrix A is 3.
Scaling Matrices

Enlarging or shrinking a vector can be done by multiplying the vector by the diagonal matrix of the form:
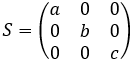
If a = b = c > 1
Then the vector is enlarging equally in all directions.
If a = b = c < 1
Then the vector is shrinking equally in all directions.
If a ≠ b ≠ c
Then the vector is scaling in different sizes in the x, y and z directions.