Intersection of circle and line
| Line | |
| Line form: y = mx + b | y = x + |
| Line form: Ax + By + C =0 | x + y + = 0 |
| Circle | |
| Circle form: (x − a)2 + (y − b)2 = r2 | ( x − )2 + ( y − )2 = 2 |
| Circle form: x2 + y2 + Ax + By + C | x2 + y2 + x + y + = 0 |
| Intersection coordinates (x1 , y1) | |
| Intersection coordinates (x2 , y2): | |
| Distance between intersection points: | |
| Distance of the line from circle center: |
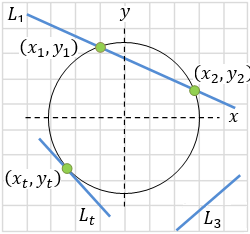
Intersection of circle and a line.

When calculating circle and line intersection the result can be one of the following posibillities:
Line L1 − Two intersection points.
Line Lt − One intersection point (line tangent).
Line L3 − No intersection exist.
If line and circles are of the form:
Line form: y = m x + d Circle form: (x − a)2 + (y − b)2 = r 2
After solving both equations we get the values for x:
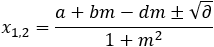
(1)
Where the value of ∂ is equal to:
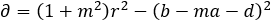
(2)
Notes:
If ∂ > 0 then two intersection points exists.
If ∂ = 0 then the line is tangent to the circle.
If ∂ < 0 then the line does not intersect the circle.
Once we found the values of x1, 2 we can substitute these values into the equation of the line to find the corresponding values of y1, 2
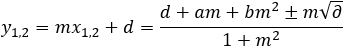
(3)
In order to find the slope of the tangent line m find the derivative value of dy/dx = m by explicite methode:
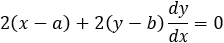
The slope m of the tangent line at point xt and yt
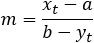
(4)
Tangent line equation:
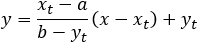
(4a)
Provided that b ≠ yt. If b = yt then the line equation become x = xt
If line and circles are of the form:
Line form: y = m x + d Circle form: x2 + y2 + A x + B y + C = 0
After solving both equations we get the values for x:
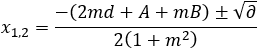
(5)
Where the value of ∂ is equal to:
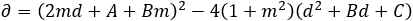
(6)
The coordinate of y1, 2 can be
determined from the line equation.
determined from the line equation.
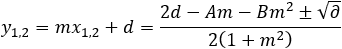
(7)
In order to find the slope of the tangent line m find the derivative value of dy/dx = m by explicite methode:
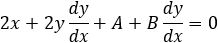
The slope m of the tangent line at point xt and yt is:
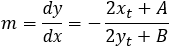
(8)
Tangent line equation:
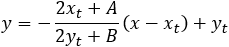
(8a)
question 1 − Find intersection points of circle: (x − 3)2 + (y + 5)2 = 9 and the
line y = −x + 1
Solution: In our case m = −1 d = 1 a = 3 b = −5 r = 3
Calculate ∂ from equation (2). ∂ = 32(1 + (−1)2) − [(−5 5 − (−1)3 − 1)]2 = 9
Beacause ∂ > 0 there are two intersection points.
By using equation (1) we find the x coordinate of the intersections:
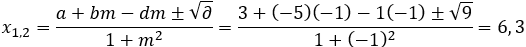
The y coordinates are found by equation of the line: y = mx + d
y1 = −6 * 6 + 1 = −5 y2 = −1 * 3 + 1 = −2
And the intersection coordinates are: (6 , −5) and (3 , −2)
question 2 − Find intersection points of circle: x2 + y2 + 3x + 4y + 2 = 0 and the
line x − 2y − 6 = 0
Solution: The line equation can be written in the form: y = 0.5x − 3
In our case: m = 0.5 d = −3 A = 3 B = 4 C = 2
Calculate ∂ from equation (6). ∂ = [2*0.5(−3) + 3 + 4*0.5]2 − 4((1 + 0.5)[(−3)2 + 4(−3) + 2] = 9
Beacause ∂ > 0 there are two intersection points.
By using equation (5) we find the x coordinate of the intersections:
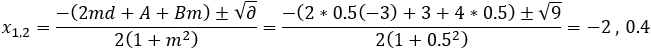
The y coordinates are found by equation of the line: y = mx + d
y1 = mx + d = 0.5*(−2) − 3 = −4
y2 = mx + d = 0.5*0.4 − 3 = −2.8
And the intersection coordinates are: (−2 , −4) and (0.4 , −2.8)
question 3 − Find the tangent line equation at point (1 , 2) to the circle: x2 + y2 + 2x + 3y − 13 = 0
Solution: From equation (8) the slope of the tangent line can be avaluated.
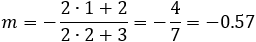
The equation of the tangent line according to (8a) is:
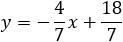
This equation can also be written in the form:
7y = − 4x + 18
