Line equation

Line equation calculator

(1) Line equation:

y =

x +

Two points on line:

x₁:

y₁:

x₂:

y₂:

Angle (α):		Intercepts: ( , 0 ): ( 0 , ):
Midpoint:	x_d:	y_d:
Line length:

Point in plane:

x_p: y_p:

The point is on the line

Distance from point (x_p, y_p) to line (1):

(2) Equation of line passing through (x_p, y_p)
and is perpendicular to line (1):

Intersection coordinates between lines
(1) and (2):

Degree Radian

Line basic definition	Line distances	Intersection point ex: 3
Basic line information	Distance from point ex: 1
Line equations	Perpendicular line ex: 2

Line basic definitions

Single line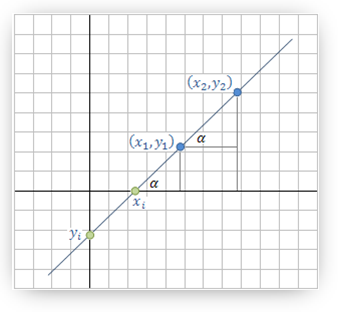 Line definition

Two lines intersection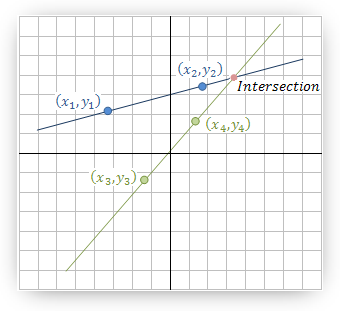

Line most general equation is of the form:

(1)

where A, B and C are any real number and A and B are not both zero. If B ≠ 0 then we can divide

equation (1) by B to obtain the normalized form of a line:

(2)

This is the equation of a line whose slope is:

and

the slope of the line (m) is defined in terms of the inclination

(3)

Note: if the angle α is greater then 90 degrees then the slope is negative.

α (0 - 90) degrees : positive slope

α (90 - 180) degree : negative slope

Necessary condition for two lines to be perpendicular to each other is that their slopes fulfill the condition:

m₁ m₂ = − 1

(4)

In order to find the intersection point of two lines we have to solve the system of linear equations representing the lines. A x + B y = −CD x + E y = −F

solution by matrix:

If the determinant:

then intersection point exists.

Basic information about line of the form y = ax + b or Ax + By + C = 0

Slope (m) of the line

m = a

y_intercept (y_i)

y_i = b

y_i = −mx_i

y_i = y₁ − mx₁

x_intercept (x_i)

tan θ

tan θ = m

Line angle (θ)
from x axis (range 0 ≤ θ < π)

θ = arctan(m)

Slope (M) of a line perpendicular to a given slope (m)

Line midpoint

Point (x, y) which divides the line connecting two points (x₁ , y₁) and (x₂ , y₂) in the ratio p:q

Point (x, y) which divides the line connecting two points (x₁ , y₁) and (x₂ , y₂) externally at a ratio p:q

Note: the (x,y) point is in the direction from point 1 to point 2,to get the other side extension change the point 1 with point 2 and vice versa

A point (x, y) which is located at a distance d from a point (x₁ , y₁) on the line

Angle θ between two lines:

Angle between two lines given by

Ax + By + C = 0

Dx + Ey + F = 0

Line equations summary

Equation of a line passing through a point (x₁ , y₁)

y = mx + ( y₁ − mx₁)

y − y₁ = m(x − x₁)

Equation of a line passing through two points (x₁ , y₁), (x₂ , y₂)

Equation of a line perpendicular to a given slope m and passing through a point (x_p , y_p)

Equation of a line perpendicular to a line which is defined by two points (x₁ , y₁) and (x₂ , y₂) and passing through the point (x_p , y_p)

Equation of a line passing through the intercepts x_i , y_i

x_iy = −y_ix + x_iy_i

Equation of a line passing through the point (x_p ,y_p) and parallel to a line which is defined by two points (x₁ , y₁) and (x₂ , y₂)

Equation of a line parallel to the line Ax + By + C = 0 and at a distance d from it.

Equation of the midline between the lines Ax + By + C = 0

Dx + Ey + F = 0

Equation of a line perpendicular to the line Ax + By + C = 0

Bx − Ay + C = 0

Equation of a horizontal line

y = b

Equation of a vertical line

x = a

Lines distances y = ax + b Ax + By + C = 0

Distance between two points (D)

Distance between intercepts x_i and y_i

Distance from a line to the origin

Distance from a line given by two points (x₁ ,y₁),(x₂ , y₂) to the origin

Distance from a line to the point
(x_p , y_p)

Distance from a line given by two points (x₁ , y₁) , (x₂ , y₂) to the point (x_p , y_p)

Distance between two parallel lines

y = ax + b

y = cx + d

Ax + By + C = 0

Dx + Ey + F = 0

Example 1 - distance from a line to a point

▲

Find the distance d of a point P(p_x , p_y) to the line given by the equation Ax + By + C = 0.
Calculate the numerical value of the distance between point (2 , −3) and line y = 4x − 5

We draw at point P a parallel line to the given line (dashed line).

Then we draw a line PF between the points P and F. This line is perpendicular to the given line.

The slope m of the given line is:	m = −A / B
The slope M of line PF is:	M = −1 / m = B / A

In order to make calculations easier we draw another line QS starting from the origin and parallel to line PF.

The general equation of a line passing through a point is given by: y = mx + y₁ − mx₁

The equation of line PQ passing through point (p_x , p_y) is:

Equation of line QS passing through the origin is:

Point Q is the intersection of lines PQ and QS. Solving this equations by substituting the value of y we get:

And finally, we get:

and

Point S is the intersection point of the two lines

Ax + By + C = 0

and

Solving for S_x and S_y we get

and

The distance d is the distance between the two points Q and S given by the points:

Q((A^2 p_x+ABp_y)/(B^2+A^2 ),(ABp_x+B^2 p_y)/(B^2+A^2 ))

and

d=√(((A^2 p_x+ABp_y)/(B^2+A^2 )+AC/(A^2+B^2 ))^2+((ABp_x+B^2 p_y)/(B^2+A^2 )+BC/(A^2+B^2 ))^2 )

d=√(A^2 (Ap_x+Bp_y+C)^2+B^2 (Ap_x+Bp_y+C)^2 )/(A^2+B^2 )

d=√((Ap_x+Bp_y+C)^2 (A^2+B^2 ) )/(A^2+B^2 )

The given line can be written in the standard form as 4x − y − 5 = 0

So, we have: A = 4 B = −1 and C = −5 p_x = 2 p_y = −3

Substituting these values into the distance equation we get the final solution:

d=|4∙2+(-1)(-3)-5|/√((4^2+(-1)^2 ) )=|8+3-5|/√17=6/√17=1.46

Example 2 - line from point to perpendicular line

Print line from point to perpendicular line example

▲

Find the equation of the line passing through the point (3 , − 1) and is perpendicular to the line
2x − y − 1 = 0

The slope of the perpendicular line is:

y = 2x − 1

→

m = 2

The slope of the line perpendicular to the given line and passing through the point is:

The equation of the line passing through the point (3 , − 1) is:

y = Mx + (y₁ − Mx₁)

x + 2y − 1 = 0

If the intersection point of both lines is needed then we have to solve the equations:

x + 2y − 1 = 0

2x − y − 1 = 0

From the first equation x is	x = 1 − 2y
Substitute x into the second equation	2(1 − 2y) − y − 1 = 0
And the intersection coordinate is	(0.6 , 0.2)

Example 3 - intersection point of perpendicular lines

Print intersection point between line and point example

▲

Find the intersection point of the line 2x − y = 0 and the line passing through the point (5 , 2) and is perpendicular to the given line.

If the line form is given by: Ax + By + C = 0

The slope of the given line is:

m = − A/B

Slope of the line perpendicular to the given line is:

The equation of the line passing through the point (P_x , P_y) = (5 , 2) (green line) and is perpendicular to the given line is:

y = Mx + (P_y − MP_x)
	(1)
y = −0.5x + 2 + 0.5‧5	(2)
x + 2y − 9 = 0

In order to find the intersection point (N_x , N_y) we have to solve equation (1) and the given line this can be done in direct substitution or by Cramer’s law:

From equation (1) We have
Substitute y into equation (1)
Solving for x we get
And y is equal to

The general intersection of a line and the perpendicular line that passes through a point is:

((B^2 P_x-ABP_y-AC)/(A^2+B^2 ) ,-1/B [(〖AB〗^2 P_x-A^2 BP_y-A^2 C)/(A^2+B^2 )-C])

(3)

The given values are A = 2 B = −1 C = 0 P_x = 5 P_y = 2
Solving the numerical values, we have	x + 2(2x) − 9 = 0
	x = 9/5 = 1.8
and y is equal to	y = 18/5 = 3.6