☖ Home ⇄ Units Converter ⧉ Geometry Σ Math ✈ Physics 〶 Electricity

Distance between two 3D lines calculator

Print distance between two 3D lines
Parametric line equation L1
x
 = 
 + t 
y
 = 
 + t 
z
 = 
 + t 
L2
x
 = 
 + s 
y
 = 
 + s 
z
 = 
 + s 
General line equation L1
 x
+
=
 y
+
=
 z
+
L2
 x
+
=
 y
+
=
 z
+
Lines defined
by 4 points		 L1
x1
 
   y1
 
   z1
 
x2
 
   y2
 
   z2
 
L2:
x3
 
   y3
 
   z3
 
x4
 
   y4
 
   z4
 
Distance between the lines:
 
Connecting line intersections:
 
Values of  t  and  s:
 
Angle between the lines:
 
Connecting line vector (n):
 
Connecting line unit vector:
 
       
Steps to calculate distance between two 3D lines
Presentation of 3D lines
Unique cases
3D lines - Example 1
Example 2
Example 3
Example 4

Steps to calculate the distance between two 3D lines

Print circle and line intersection
Finding the distance d between two 3D lines L1 and L2 that are given by the parametric equations:
L1:
L2:
The lines can also be described as:
L1 = r1 + t e1
L2 = r2 + s e2
Step (1)
Calculate the cross product of the direction numbers   e1 = (a1, b1, c1) and   e2 = (a2, b2,  c2).   n = e1 ✕ e2.  The result is a vector perpendicular to both lines (i, j, k  are the vector notation in the  x, y,  and  z  direction).:
Note: if e1 ✕ e2 = 0 then the lines are parallel, and this method of calculation is not applicable.

Step (2)  Find the norm of the vector (is a scalar value):

Step (3)  The unit vector in this direction is:
Step (4)  Find a point  P  on  L1  where  t = 0:
Step (5)  Find a point  Q  on  L2  where  s = 0:

Step (6)  Find vector  PQ  connecting  P  to  Q  by subtracting  (Q ⎯ P):

PQ=i(x_1-x_0 )+j(y_1-y_0 )+k(z_1-z_0 )
Step (7)
The absolute value of the dot product of vector  n  with PQ and divide by the norm of  |n|  will give the required distance d between the lines:
D=(n∙PQ)/|n|
D=|((b_1 c_2-b_2 c_1 )(x_2-x_1 )-(a_1 c_2-a_2 c_1 )(y_2-y_1 )+(a_1 b_2-a_2 b_1 )(z_2-z_1 ))/√((b_1 c_2-b_2 c_1 )^2+(a_1 c_2-a_2 c_1 )^2+(a_1 b_2-a_2 b_1 )^2 )|
Step (8)
The shortest line intersections parameters values, (when the lines are not intersecting each other are):
t=((e_2×n)∙(r_2-r_1 ))/(n∙n)=((e_2×n)∙PQ)/(n∙n) s=((e_1×n)∙(r_2-r_1 ))/(n∙n)=((e_1×n)∙PQ)/(n∙n)

Unique cases

Print Example 3

Given two lines with two same axis direction numbers equal to 0, in this case the x and y axis. This indicates that all x and y points of both lines are constant and therefore parallel to the z axis.

L_1=(■(x_1@y_1@z_1 ))+t(■(0@0@c_1 )) L_2=(■(x_2@y_2@z_2 ))+s(■(0@0@c_2 ))

Two parallel lines
From the drawing we see that both lines (green points directed to us) in the x-y plane. it is obvious that the distance between the lines will be:
D=√((x_2-x_1 )^2+(y_2-y_1 )^2 )

The same way we can find the distance between two lines that are parallel to the y and z axis.

Let analyse the case that the none 0 axes are not in the same direction L1 and L2.

L_1: (■(x@y@z))=(■(x_1@y_1@z_1 ))+t(■(0@0@c_1 )) L_2: (■(x@y@z))=(■(x_2@y_2@z_2 ))+s(■(0@b_2@0))

Two parallel lines3D view
Two parallel linesView along z axis

From the drawing we can see that line L1 is located parallel to the z axis and line L2 is parallel to y axis. Therefore, the angle between the lines is 90 degree and the distance between the lines is simply

D=x_2-x_1

Based on the example above we can derive the distance equations for other similar combinations of direction numbers:

L_1: (x,y,z)=(x_1,y_1,z_1)+t(0,0,c_1 ) L_2: (x,y,z)=(x_2,y_2,z_2)+t(0,b_2,0)
D=y_2-y_1
L_1: (x,y,z)=(x_1,y_1,z_1)+t(0,b_1,0) L_2: (x,y,z)=(x_2,y_2,z_2)+s(a_2,0,0)
D=z_2-z_1
L_1: (■(x@y@z))=(■(x_1@y_1@z_1 ))+t(■(a_1@b_1@0))
In this case only the z direction number is zero. hence all the points of the line are located on the plane parallel to the x-y plane, where z = z1. The distance between the lines can be found by the steps described earlier.

Two lines will be parallel in space when all three direction numbers are the same:

a1 = a2     and     b1 = b2     and     c1 = c2

3D lines - Example 1

Print Example 3
Question:
Find the distance between the lines:   L1: x = 3 + 4t,  y = − 2,  z = 5 − 2t   and the line   L2: x = 3 + s,  y = 2 + 2s,  z = − 1 + 7s.
Solution:
Step (1)   Cross product of the direction numbers is:

Step (2)   The norm of the vector is:

Step (3)   The unit vector in the line direction is:
Step (4)   A point P on L1 where t = 0 is at:    (3, ⎯ 2, 5)

Step (5)   A point Q on L2 where s = 0 is at:    (3, 2, ⎯ 1)

Step (6)   (Q ⎯ P) = (0, 4 ⎯ 6)

Step (7)   Finally the distance between the lines is:

3D lines - Example 2

Print Example 3
Question:
Find the intersection point of the lines:

(x+3)/2=y/4=(z+2)/3 (x-4)/1=(y-1)/(-11)=(z-3)/(-4)

Solution:
We will solve the problem by two ways first we shall write the parameterized equations of the line:
L_1: (■(x@y@z))=(■(-3@0@-2))+t(■(2@4@3)) L_2: (■(x@y@z))=(■(4@1@3))+s(■(1@-11@-4))

Because the x and y coordinates of the intersection point of lines L1 and L2 are the same, we can find the values of s and t.

x:     −3 + 2t = 4 + s
y:       0 + 4t = 1 −11s
x:      2t − s = 7
y:      4t + 11s = 1

Now solving by Cramer's rule or by substitution we get:

t=|■(7&-1@1&11)|/|■(2&-1@4&11)| =78/26=3 s=|■(2&7@4&1)|/|■(2&-1@4&11)| =(-26)/26=-1

Once we fount the values of t and s the only thing remained is to check if the values of z in both lines are equal if yes then the lines intersect.

L2 z: −2 + 3 * 3 = 7 and L2 z: 3 + 4 = 7       so the lines intersect.

To find the intersection point, we can substitute the value of  t = 3  into the parametric equation to get:  Pi (3, 12, 7).

Another way to solve the problem is to calculate the distance between the lines, if the distance is 0 then the lines intersect.

The vectors of the points on the line and the direction numbers are:

r1 = (−3, 0, −2)       r2 = (4, 1, 3)       e1 = (2, 4, 3)       e2 = (1, −11, −4)

The vector in the direction of the shortest line (perpendicular to both lines) is:

The unit vector in this direction is:

The connecting vector between the points of both lines is:

PQ = r2 − r1 = (4 + 3, 1 − 0, 3 + 2) = 7i + j + 5k

Now the only step remains is to find the distance between the lines is to project PQ to the shortest line direction:

d=(7i+j+5k)∙(0.52i+0.33j-0.79k)=0

As expected, we get 0 distance and the lines are intersecting each other.

3D lines - Example 3

Print Example 3
Question:
Find the distance between the lines:

L_1: (■(x@y@z))=(■(6@8@4))+t(■(6@7@0)) L_2: (■(x@y@z))=(■(6@8@2))+t(■(6@8@4))

Solution:

The vectors of the points on the line and the direction numbers are:

r1 = (6, 8, 4)       r2 = (6, 8, 2)       e1 = (6, 7, 0)       e2 = (6, 8, 4)

The vector in the direction of the shortest line (perpendicular to both lines) is:

n=e_1×e_2=|■(i&j&k@6&7&0@6&8&4)|=28i-24j+6k

The unit vector in this direction is:

n ̂=n/|n| =(28i-24j+6k)/√(28^2+24^2+6^2 )=0.749i-0.642j+0.161k

The connecting vector between the points of both lines is:

PQ = r2 − r1 = (6 − 6, 8 − 8, 2 − 4) = 0i + 0j + −2k

Now the only step remains is to find the distance between the lines is to project PQ to the shortest line direction:

d=(0i+0j+2k)∙(0.749i-0.642j+0.161k)=0.32

3D lines - Example 4

Print Example 4
Question:
Find the distance and the intersection points of the shortest line of the lines:
L1:   x = 1 + 3t,   y = 3 + t,   z = −2t    and the line
L2:   x = 1 + s,   y = −1,   z = 5 − 2s
Solution:

Any arbitrary point along the line   L1 is     P = (x, y, z) = (1 + 3t,   3 + t,   −2t):

And point along the line   L2 is   Q = (x, y, z) = (1 + s,   −1,   5 − 2s):

The vector connecting these two arbitrary points is:

PQ = Q - P = [1 + s − (1 + 3t), −1 − (3 + t),   5 − 2s − (2t)]

PQ = (s − 3t , −4 − t , 5 − 2s + 2t)

The shortest line will be the vector PQ which is perpendicular to both lines direction numbers e1 and e2, the values of t and s will assure us that line PQ is the shortest line despite the fact that we choose initially two arbitrary points on both lines L1 and L2 to calculate PQ, from the dot product we have the values:

PQ ⟘ e1 = PQ • e1 = 0       and       PQ ⟘ e2 = PQ • e2 = 0

e1 = (3, 1, −2)       e2 = (1, 0, −2)

(s − 3t , − 4 − t , 5 − 2s + 2t) ‧ (3, 1, −2) = 0

(3s − 9t − 4 − t − 10 + 4s −4t) = 0

14t − 7s = −14

(s − 3t , −4 − t , 5 − 2s + 2t) ‧ (1, 0, −2) = 0

(s − 3t + 0 − 10 + 4s − 4t) = 0

7t − 5s = −10

And we get two equations with the unknowns t and s. After solving this equations, we get the values:

t = 0   and   s = 2.

Substituting these values into the vector PQ we get:   PQ = (2 , −4 , 1)

The length of PQ is the shortest distance between the lines:

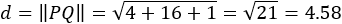
d=‖PQ‖=√(4+16+1)=√21=4.58

The points of intersection of the shortest line with line L1 and L2 are:

L1: (1 , 3 , 0)   and   L2: (3 , −1 , 1)

Another way to solve the problem is to find the vector perpendicular to both given lines by cross product their direction numbers:

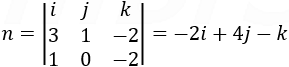
n=|■(i&j&k@3&1&-2@1&0&-2)|=-2i+4j-k

The unit vector in the  n  direction is:
n ̂=n/‖n‖ =-2/√21 i+4/√21 j-1/√21 k

To find the vector PQ we choose any two arbitrary points along the lines L1 and L2 let say:   t = 0   then (1 , 3 , 0) and s = 0   then (1 , −1 , 5).

PQ = (1 − 1 , 3 + 1 , 0 −5) = (0 , 4 , −5)

The shortest line length is the projection of PQ on the unit vector (
PQ∙n ̂
).

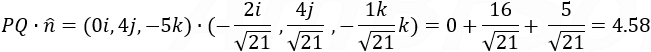
PQ∙n ̂=(0,4,-5)∙(-2/√21 ,4/√21 ,-1/√21 k)=0+16/√21+ 5/√21=4.58