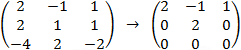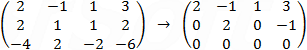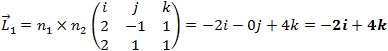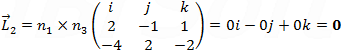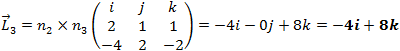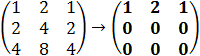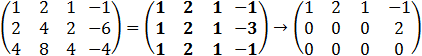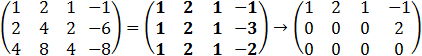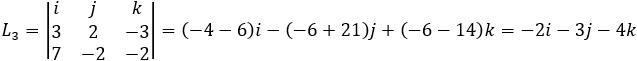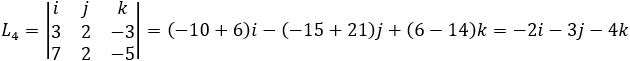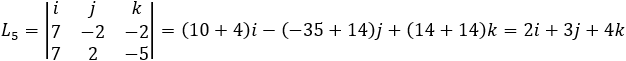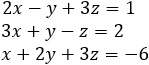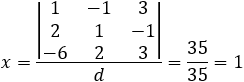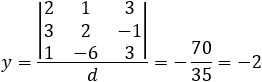Intersection of three planes

Intersection of 3 planes calculator

Plane 1:	x +	y +	z +	= 0
Plane 2:	x +	y +	z +	= 0
Plane 3:	x +	y +	z +	= 0

Plane defined by 3 points:	x₁	y₁	z₁
	x₂	y₂	z₂
	x₃	y₃	z₃
Plane equation:

Intersection type:

Intersection coordinate:

det + rank:

NOTES:

Intersection line 1 equation:

Intersection line 2 equation:

Intersection line 3 equation:

n₁ x n₂ | Angle

n₁ x n₃ | Angle

n₂ x n₃ | Angle

Intersection of 3 planes summary Example 1 Example 2 Example 3 Example 4

Intersection of 3 planes summary

Three planes intersection.

Plane 1: A₁ x + B₁ y + C₁ z = D₁

Plane 2: A₂ x + B₂ y + C₂ z = D₂

Plane 3: A₃ x + B₃ y + C₃ z = D₃

Normal vectors to planes are:

n₁ = iA₁ + jB₁ + kC₁

n₂ = iA₂ + jB₂ + kC₂

n₃ = iA₃ + jB₃ + kC₃

For intersection line equation between two planes see two planes intersection.

In order to find which type of intersection lines formed by three planes, it is required to analyse the ranks R_c of the coefficients matrix and the augmented matrix R_d.

Rank:

Rank:

If vectors: n₁ × n₂ = 0 then the planes are parallel (cross product).

The angle between two planes from the vectors dot product is:

	Plane - P₁
	Plane - P₂
	Plane - P₃

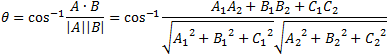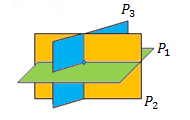
Condition for a single point of intersection is:

rank R_c = 3
rank R_d = 3

Intersection point is given by Cramer's rule:

In vector analysis: n₁ · (n₂ × n₃) ≠ 0 (Example 4)

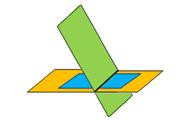Condition for one line intersection (two coincide planes) are:

rank R_c = 2 and R_d = 2

In vector analysis: n₂ × n₃ = 0 n₁ × n₃ = n₁ × n₂ ≠ 0

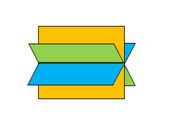Condition for one line intersection is: (Example 3)

rank R_c = 2 and R_d = 2

In vector analysis: n₁ × n₂ = n₁ × n₃ = n₂ × n₃ ≠ 0

Note: n₁ is the same as −n₁ but pointing to the opposite direction.

The reason for this is the fact that: n₁ × n₂ = −n₂ × n₁

Condition for two lines intersection (two parallel planes) is:

rank R_c = 2 and R_d = 3

In vector analysis: n₂ × n₃ = 0 n₁ × n₃ = n₁ × n₂ ≠ 0

Condition for three lines intersection is:

rank R_c = 2 and R_d = 3

All values of the cross product of the normal vectors to the planes are not 0 and are pointing to the same direction.

n₁ × n₂ = n₁ × n₃ = n₂ × n₃ ≠ 0

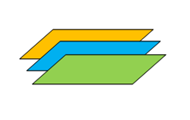
Condition for no intersection (three parallel planes) are:

rank R_c = 1 and R_d = 2

Check number of similar planes R_s: R_s = 0 (Example 2)

In vector analysis: n₁ × n₂ = n₁ × n₃ = n₂ × n₃ = 0

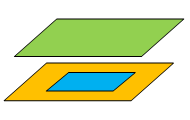
Condition for no intersection (three parallel planes, 2 coincides) are:

rank R_c = 1 and R_d = 2

Check number of similar planes R_s: R_s = 2 (Example 2)

In vector analysis: n₁ × n₂ = n₁ × n₃ = n₂ × n₃ = 0

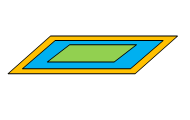
Condition for no intersection (three coincide planes) are:

rank R_c = 1 and R_d = 1

In vector analysis: n₁ × n₂ = n₁ × n₃ = n₂ × n₃ = 0

The cross product is equal to:

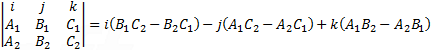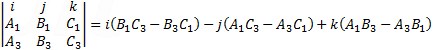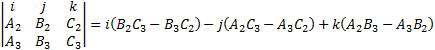Example 1 - Intersection of 3 planes

Investigate the intersection values between the three planes:
	Plane 1: 2x − y + z + 3 = 0
	Plane 2: 2x + y + z + 2 = 0
	Plane 3: − 4x + 2y − 2z − 6 = 0

First find the rank of the coefficient matrix by upper triangularization.

	R_c = 2
	R_d = 2

The ranks can be found by two steps, first subtract the second row from the first row and then the second step is to subtract the fourth row from the first row multiplied by two.

If we look on the augmented matrix, we see that we have two equations with three unknowns so we can choose one value for example z = t and because B₁/D₁ ≠ 0 we have the solution for y the value y = 0.5 now the value of x will be from the first raw:

2x - y + z = -3

x = (y - z -3)/2

x = (0.5 -t -3)/2 = -1.25 - 0.5t

Thus is a line presented pay parameter t:

L{x,y,z}={− 1.25 − 0.5t, 0.5, t} same as {− 1.25 − t, 0.5, 2t} After multiplying both t by 2.

We could find the intersection line by vectors calculation, the planes are described by the vectors in i, j and k direction

n₁ = 2i − j + k

n₂ = 2i + j + k

n₃ = − 4i + 2j − 2k

Now we can perform the cross product on each pair of the vectors.

L₂ is equal to 0 that is because the two plans 1 and 3 are parallel.

We also see that lines L₁ and L₂ are pointing to the same direction − 4i + 8k = − 2i + 4k (vectors can be factored without changing their direction).

Now that we have the intersection line direction, we need a point on the line in order to set the line equation, because R_d = 2 we must have the value of y from the R_d matrix: y = 1/2 = 0.5

now we can choose an arbitrary value to z let say z = 0 than x = − 1.25t or parametric line equation:

L{x,y,x} = {− 1.25 − 2t, 0.5, 4t}

Because R_c = 2 and R_d = 2 then two planes are parallel and because one cross product of the vectors are 0 the intersection looks like:

The angle between plane 1 and plane 2 is found from the dot product: A · B = |A||B| cos θ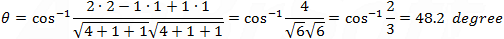

Example 2 - Intersection of 3 parallel planes

Given three planes by the equations: x + 2y + z − 1 = 0 2x + 4y + 2z − 6 = 0 4x + 8y + 4z − n = 0
Determine the locations of the planes to each other in the case that n = 4 and second time n = 8.

The matrix of the x y and z coefficients after multiplying first row by 2 and subtracting from second row and then multiplying first row by 4 and subtracting from third row we get the matrix:

Rank R_c = 1 we see that all the planes are parallel

(1)

In order to find the number of coincides planes we have to analyse the augmented matrix with n = 4 after dividing second row by 2 and third row by 4 and repeating the process done on the coefficient’s matrix, we get the matrix:

Rank R_d = 2

(2)

In the case that n = 8 we have the augmented matrix:

Rank R_d = 2

(3)

We can clearly see that if we get R_d = 2 we have to check for similar planes in order to find the number of coincides planes, from the centre matrix (2) we see that the first and third planes are coincides so R_s = 2, from the centre matrix (3) we see that all the planes are distinct R_s = 3

Notice: If all the planes are similar then R_d = 1 and we don't have to check for planes similarity.

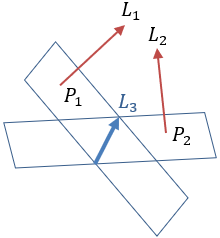
Example 3 − Line intersection of three planes

Given the three planes P₁: 3x + 2y − 3z − 10 = 0 P₂: 7x − 2y − 2z − 5 = 0 P₃: 7x + 2y − 5z − 16 = 0 Show that all three planes have a common intersection line.

Let first analyse the intersection of two planes.
L₁ and L₂ are both perpendicular to planes P₁ and P₂ respectively, so the direction numbers of those lines are given by the attitude numbers of the planes.
In vector notation we have:

L₁ = a₁x + b₁y + c₁z and L₂ = a₂x + b₂y + c₂z

We can find the direction of the intersecting line L₃ by cross product of vectors L₁ and L₂ so: L₃ = L₁ × L₂ = P₁ × P₂

L_3=|■(i&j&k@3&2&-3@7&-2&-2)|=(-4-6)i-(-6+21)j+(-6-14)k=-2i-3j-4k

Now we can perform the same test on the pair of planes P₁ and P₃

L_4=|■(i&j&k@3&2&-3@7&2&-5)|=(-10+6)i-(-15+21)j+(6-14)k=-2i-3j-4k

And the same way the pair P₂ and P₃

L_5=|■(i&j&k@7&-2&-2@7&2&-5)|=(10+4)i-(-35+14)j+(14+14)k=2i+3j+4k

Notice that all the intersection lines L₃ , L₄ and L₅ has the same direction numbers values. So, they are at least parallel lines, the negative values indicate the same orientation of the line but in the opposite direction. Now we have to prove that all the lines coincide. So, we have to show that all the planes have a common line intersection. Writing the planes in set of equations we get:

{■(3&2&-3@7&-2&-2@7&2&-5)}{■(x@y@z)}={■(10@5@16)}

The augmented matrix is
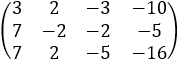After few steps on the rows, we get:

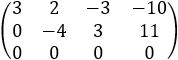we can see that the rank of the augmented triangular matrix R_d and the coefficients matrix R_c are: rank = R_c = R_d = 2 This case is described in the table. This means that we have a set of three unknowns and only two equations. So, we can solve this case by setting the value of y = t.

Then −4t + 3z = 11 and z = 4t/3 − 11/3 and x = 2t/3 − 1/3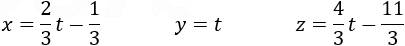

$$ x = {2t \over 3} - {1 \over 3}$$

$$ y = t$$

$$ z = {4t \over 3} - {11 \over 3}$$

These values represent a single line that intersects all the three planes. By inserting any value for t we can find points along this line for example.

t = 0	(-1/3 , 0 , -11/3)
t = 1	(1/3 , 1 , -7/3)

Example 4 − Three planes point intersection

Find the intersection point of the three planes given by the equations 2x − y + 3z − 1 = 0
3x + y − z − 2 = 0 and x + 2y + 3z + 6 = 0.

The first step is to check if a single intersection point exists this happens when the rank of the coefficients R_c = 3 matrix and the augmented matrix R = 3 is 3, (see table).

At the intersection point the values of x, y and z are the same for the three planes, so we have 3 equations and 3 unknowns to solve.

Solving the set of equations by Cramer's rule we get:
The determinant of the coefficient’s matrix is

And the single point of the intersection of the three planes is: (1 , −2 , −1)