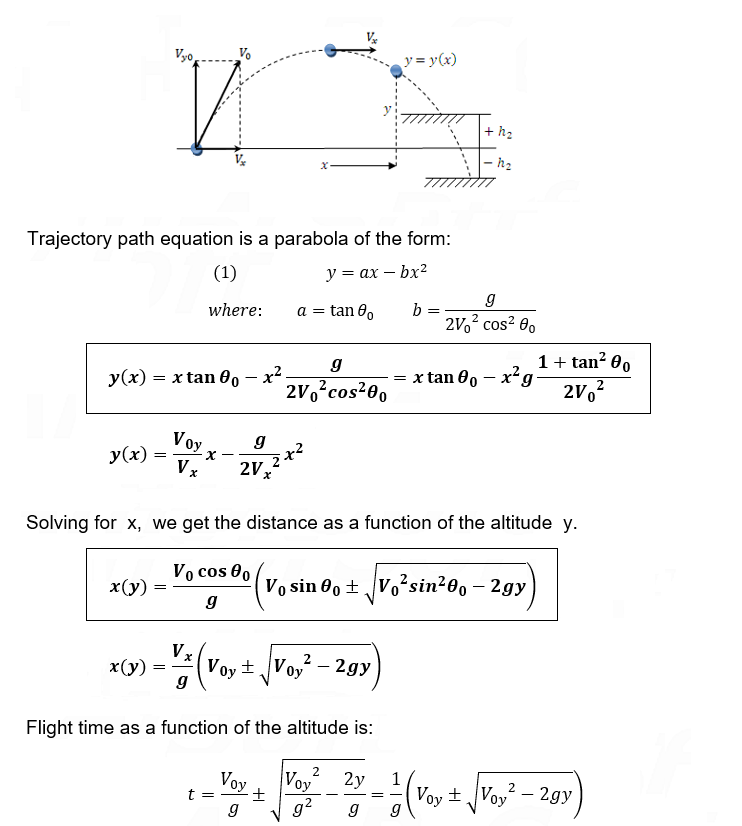
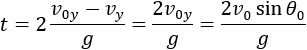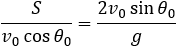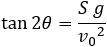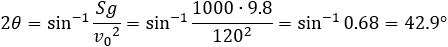Projection balistic calculator

Acceleration Downward trajectory Free fall

Horizontal trajectory
Trajectory path equation
Input table equations

Example 1 - projection path
Example 2 - projection angle

Projection calculator

*Input 2/3/4 values in any allowed fields

System of units:

Example: A projectile has an initial velocity of 12 m/s² at an angle of 30°, it hits the ground at the end at an elevation of minus 1 m bellow the initial height, find projection distance, and flight time.

Final elevation point at ground level

Initial velocity (V₀ ):

Trajectory angle (θ₀ ):

Trajectory distance (S):

Horizontal velocity (V_x ):

Vertical initial velocity (V_0y ):

Total travel time (T):

Maximum height reached (H):

Projection values at selected locations during flight

Relative elevation (h_t):

Relative projection angle (θ_t ):

Relative projection distance (S_t):

Relative vertical velocity:(V_ty ):

Relative trajectory velocity: (V_t ):

Relative travel time (T_t ):

Input limit:

Trajectory path equation:

Horizontal projection summary equations

With no air resistance, winds or other disturbances the ideal horizontal velocity V_x is the same during the entire motion and resembles a parabola.

Earth gravity acceleration g is directed to the center of the earth and is equal to:

g = −9.80665 m/s²

Summary of useful equations

Projection parabola path equation

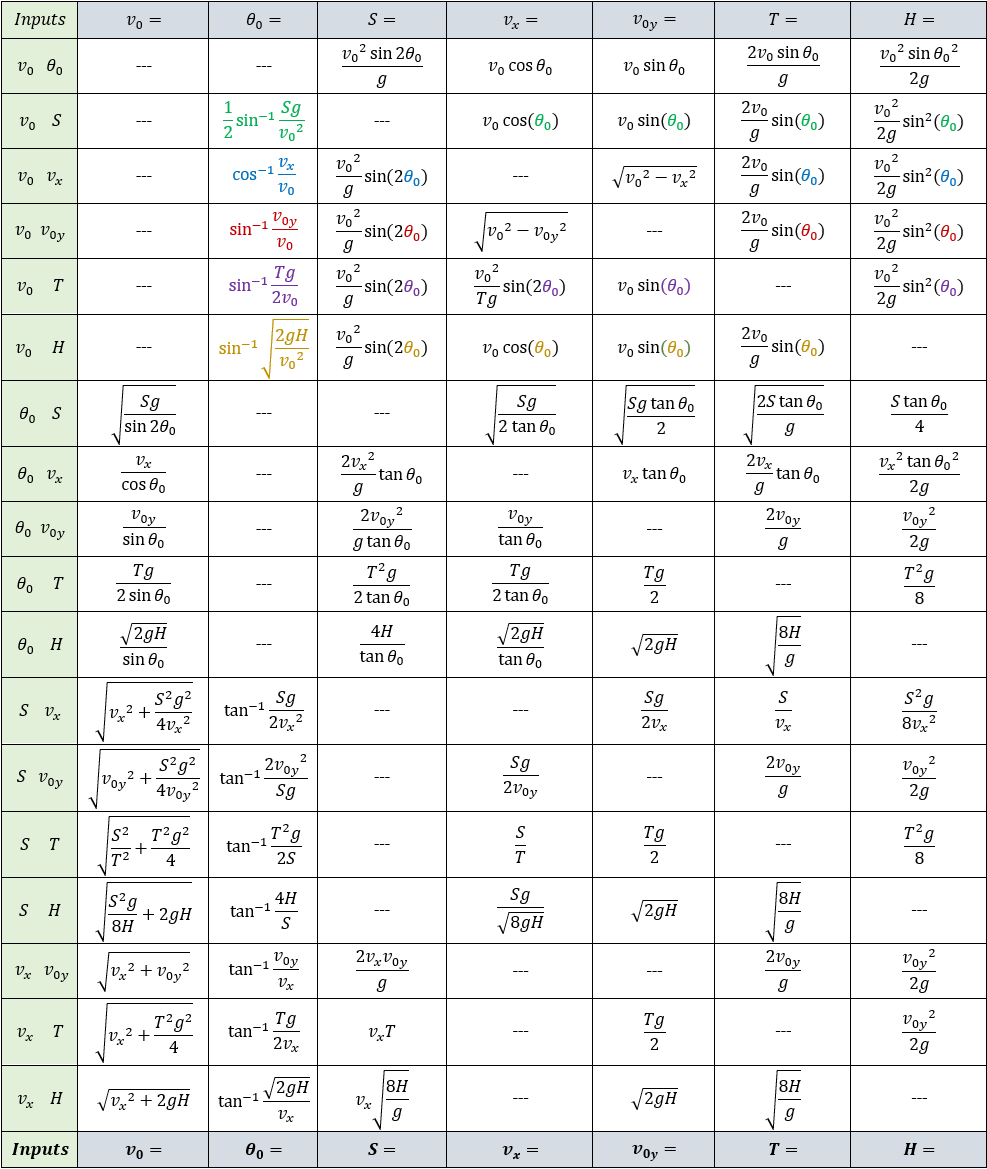
Calculations table of different inputs

* The values are presented for a complete flight cycle to reach the same altitude at the end of the motion, vertically it mean up to the highest point and back to the initial height.
**provide the relation between the x and y coordinates at any point of time in the motion of the projectile.

Example 1 - path equation

Find the trajectile motion equation, and find the elevation of an object after passing a distance of 200 m in the x direction if it leaves a nozzle at a valocity of 50 m/s and at an angle of 35°.

In the x direction the acceleration of the object is zero therfore the velocity is constant and is equal to the initial velocity multiplyed by cosθ:

v_x = v₀ cosθ₀

The displacement in the x direction described by constant speed is:

(1)

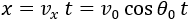
the velocity in the y direction is the component of the initial velocity v₀ in the y direction;

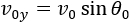
v_0y=v_0 sin⁡〖θ_0

The vertical dicplacement is calculated according to the free fall equations and replacing h by the value y.

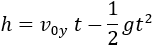
h=v_0y t-1/2 gt^2

(2)

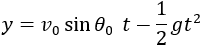
To establish an equation that the values of y and x are bound together, we will substitute the value of t from equation (1) into equation (2) to get the equation:

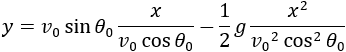
y=v_0 sin⁡〖θ_0 x/(v_0 cos⁡〖θ_0 〗 )〗-1/2 g x^2/(〖v_0〗^2 cos^2⁡〖θ_0 〗 )

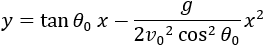
y=tan⁡〖θ_0 x-g/(2〖v_0〗^2 cos^2⁡〖θ_0 〗 )〗 x^2

(3)

Now we substitute the given values to equation (3) to find the elevation of the object after horizontal distance of 200m.

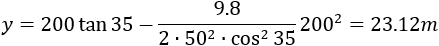
y=200 tan⁡35-9.8/(2∙50^2∙cos^2⁡35 ) 200^2=23.12m

Example 2 - angle of projection

Find the angle that a catapult should fire an object at an initial velocity of 120 m/s² if it should hit the ground at a distance of 1km away, the value of g is 9.8 m/s².

We know that vx and vy0 are equal to

v_x = v₀ cos θ

and

v_y0 = v₀ sin θ

From the projectile distance and v_x we can calculate the flight time.

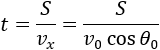
t=S/v_x =S/(v_0 cos⁡〖θ_0 〗 )

The flight time can be calculated from V_0y and the fact that at the top the velocity V_y = 0 (the total flight time will be twice the value of t, because it contains the motion upward and then back to earth) therfore using the free fall equations we have:

t=2 (v_0y-v_y)/g=(2v_0y)/g=(2v_0 sin⁡〖θ_0 〗)/g

Comparing the two flight times we get:

From the equation the angle is equal to:

Example 2

θ=42.9/2=21.45°