Horizontal projection calculator

Acceleration Free fall Projection

Motion equations Table of inputs calculations Detail solution 1 Detail solution 2

Horizontal downward projection

*Input 3 values in any allowed fields

System of units:

Run

Initial incline velocity (V₀ ):
Projection initial angle (θ₀ ):
Horizontal velocity (V_x ):
Vertical initial velocity (V_0y ):

Projection distance (S):
Total travel time (T):
Vertical distance (H):
Vertical final velocity (V_t ):
Vertical final velocity (V_ty ):
Projection final angle (θ_t ):

Input limit:
Projection path equation:

The downward projection combines two motions, constant speed in the x direction and free fall in the downward y direction. The motion equations are:

In the x direction:

In the y direction:

The path of the downward projection describes the right half of the parabola and is:
(the equation is derived from the general equation of motion of a projection θ₀ = 0)

The signs of the variables should follow the rules

Positive values:

V_x

V₀

V_t

Negative values:

−θ₀

−θ_t

−V_0y

−V_ty

−H

−g

Example of detailed solution

An object is launched downward at an angle of -35° degree and initial velocity of 12 m/s. Find all the parameters at the point that the object has a velocity of V_t = 25 m/s.

From the question we have the values of:

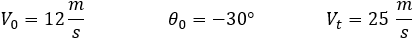
V_0=12 m/s θ_0=-30° V_t=25 m/s

The horizontal velocity is equal to:

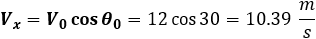
V_x=V_0 cos⁡〖θ_0 〗=12 cos⁡〖30=10.39 m/s〗

The downward initial velocity is calculated from:

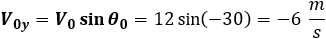
V_0y=V_0 sin⁡〖θ_0 〗=12 sin⁡〖30=6 m/s〗

The downward final velocity is calculated from:

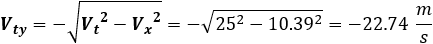
V_ty=√(〖V_t〗^2-〖V_x〗^2 )=√(25^2-〖10.39〗^2 )=22.74 m/s

Next we can find the value of the time T:

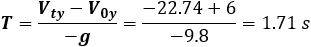
T=√((V_ty-V_0y)/(-g))=√((-22.74+6)/(-9.8))=1.31 s

Now we can find the horizontal distance made by the object:

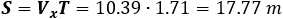
S=V_x T=10.39∙1.31=13.61 m

The total vertical drop height made by the object:

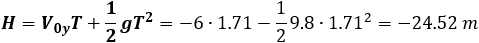
H=V_0y T+1/2 gT^2=-6∙1.31-1/2 9.8∙〖1.31〗^2=-16.27 m

Finaly the angle at the end point is:

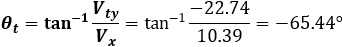
θ_t=〖tan〗^(-1)⁡〖V_ty/V_x 〗=tan^(-1)⁡〖(-22.74)/10.39〗=-65.44°

Example of detailed solution - 2

An object is launched downward at an angle of −60° degree and initial velocity of 18 m/s. Find all the parameters at the point that the object reach an angle of θ_t = −76°.

From V₀ and θ₀ the horizontal velocity V_x can be found:

V_x=V_0 cos⁡〖θ_0 〗=18 cos⁡〖60=9 m/s〗