|
Tangent points from a point
(xp , yp) on a circle.
Example: Find the tangent points on the circle (x − 2)2 + (y + 5)2 = 9 from point (7 , 1).
In this case: a = 2 b = − 5 r = 3
The value of the square root is:
x1 = 4.87 x2 = 0.61
y1 = − 5.89 y2 = − 2.34
So first tangency point is:
(4.87,-5.89) and the second point is the other points: (0.61,-2.34)
Now we can check if the tangent point that we found is on the circle:
(4.866-2)2 + (-5.888 + 5)2 =
2.8662 + (-.888)2 = 9
Note: we used higher precision of the point coordinate otherwise we would get slightly different value then 9.
nomenclature:
| D − | Distance from point to circle center |
| d − | Distance from point to tangent point |
| θ − | Angle between the two tangent lines |
| x1,2 | Tangent points x coordinates |
| y1,2 | Tangent points y coordinates |
| xi | line connecting point to
circle center x intercept |
| yi | line connecting point to
circle center y intercept |
|
The distance between the point (xp , yp) and the tangent point (1) is:
The angle between the two tangent lines θ is:
Note: in the equations above x1 can be replaced by x2.
Circle form, center at (0 , 0):
x2 + y2 = r2
Equation of the line connecting point (xp , yp) with circle center is:
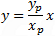
Circle form, center at (a , b):
(x − a)2 + (y − b)2 = r2
| Equation of the line connecting point (xp , yp) with circle center |
|
|
| Circle form: |
x2 + y2 + Ax + By + C = 0 |
| Equation of the line connecting point (xp , yp) with circle center |
|
|
|
 ☖ Home
⇄ Units Converter
⧉ Geometry
Σ Math
✈ Physics
〶 Electricity
☖ Home
⇄ Units Converter
⧉ Geometry
Σ Math
✈ Physics
〶 Electricity
 ☖ Home
⇄ Units Converter
⧉ Geometry
Σ Math
✈ Physics
〶 Electricity
☖ Home
⇄ Units Converter
⧉ Geometry
Σ Math
✈ Physics
〶 Electricity